|
Routine |
Typically some deep thinking required,
but not necessarily a lot of coding. |
|
Hard |
Likely involves either a multiplicity
of (possibly new) concepts or algorithms. Allow time. |
|
Buckle Up |
Start immediately, think
deeply, employ a stepwise refinement strategy and post concerns
as required. |
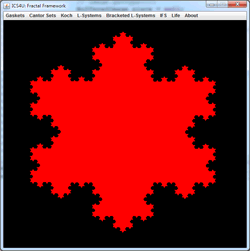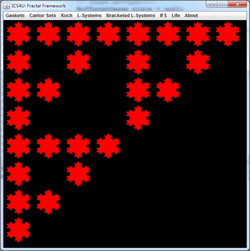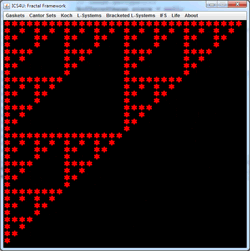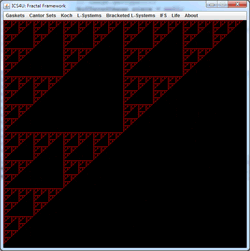
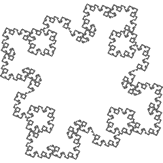
 IFS Deterministic: Iterated Function Systems.
Each iteration of the IFS Random algorithm requires the selection and application of only one affine transformation within the code, based on an array of probabilities.
IFS Deterministic: Iterated Function Systems.
Each iteration of the IFS Random algorithm requires the selection and application of only one affine transformation within the code, based on an array of probabilities.
If each
iteration of the IFS algorithm requires the application of ALL of affine transformation within the code, randomness is set aside and the outcome is predetermined. For this reason, this strategy is referred to as the Deterministic IFS algorithm.
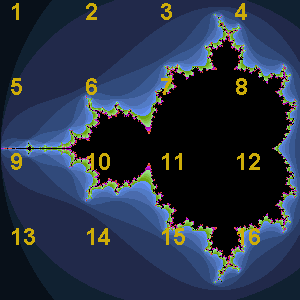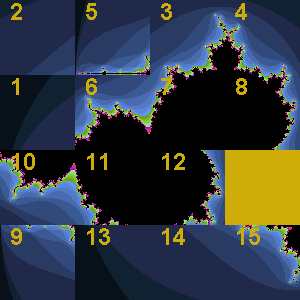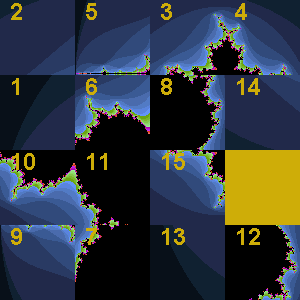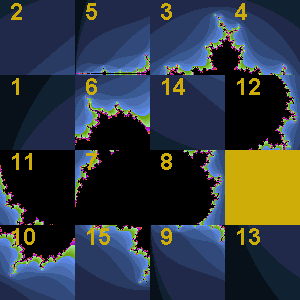
At each stage of the animation to the right, the entire panel is subjected to three affine transformations resulting in contraction mappings that yield the familiar Sierpinski gasket. What becomes clear is that regardless of the initial image, the final image (the attractor) remains predetermined. View the 2014 ACES IFSDeterministic Gallery below to verify this property.
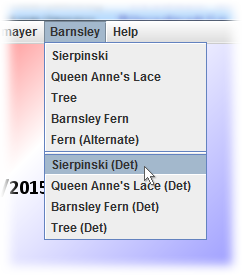
Task.
- Add a menu separator after the last IFSRandom menu item in the Barnsley menu before adding at least 4 menu items for the IFSDeterministic renderings you are about to implement (this brings the total number of entries within the Barnsley menu to 12). Visit Yale's Deterministic IFS Applet for inspiration.
 Create a class IFSDeterminstic that extends IFS along the lines of,
Create a class IFSDeterminstic that extends IFS along the lines of,
public IFDeterministic(String n, Code code, int iterations,
double distance, double xOffset, double yOffset)
that will implement the invariant or Deterministic IFS algorithm described on the Yale site.- Implement the IFSDeterministic constructor to include the creation of the following structures as discussed in class,
AffineTransform[] transforms;
AffineTransformOp[] ops;
and populate these references from the data contained in the code object.
- Revisit your favourite Catalog Activity investigated this year (I used TriadicKoch to prepare the above image). Add the method,
public BufferedImage getImage()
to this class that will return a full rendering of it as BufferedImage object. You'll use this image as the starting point for each of your preferred Deterministic IFS renderings.
- The draw method of your IFSDeterministic will exploit the AffineTransformOp object to produce the expected rendering. Specifically, you'll make use of AffineTransformOp's filter method.
- 2014 ACES IFSDeterministic Gallery...
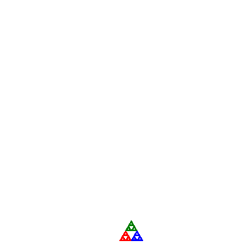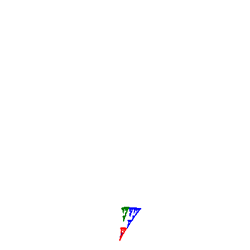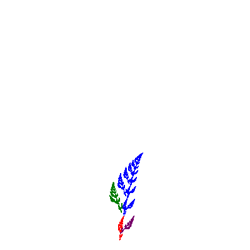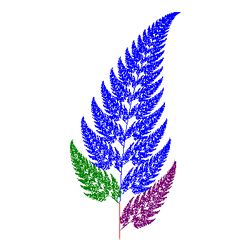
 Random IFS: Iterated Function Systems.
With the conceptual and mathematical foundations
laid, you can now undertake the final phase of this year's Catalog application to render (somewhat realistic) natural forms.
Random IFS: Iterated Function Systems.
With the conceptual and mathematical foundations
laid, you can now undertake the final phase of this year's Catalog application to render (somewhat realistic) natural forms.
Task.
- Add a second-to-last column to your Catalog application
entitled, Barnsley
- Review the IFS gallery offered through Yale's Random IFS Applet and Paul Bourke's site.
- Under the Barnsley menu, add menu items that will initiate your implementation of at least 8 images that inspire you from either of the two sites (or others you may find online).
- Add an IFS class that implements the Activity class. One
design suggestion would be to create a Code class
to encapsulate the various affine transformations, their probabilities and
the colour palette. Here's a sample,
public class IFS extends Activity {
with a constructor possibly of the form,
public IFS(String n, Code code, int iterations, double distance,
double xOffset, double yOffset)
- Create a class IFSRandom that extends IFS that will implement The Random IFS Algorithm, along the lines of,
public IFSRandom(String n, Code code, int iterations, double distance,
double xOffset, double yOffset)
- All
IFS images could be stored
in library of type TreeMap<String,Code> where String is
the name of the IFS, thereby making retrieval from within your actionPerformed() method relatively efficient. This
transforms/probability data could be encoded within the constructor of the Content class. Here's a sample,
library.put("SierpinskiIFS", new Code(new double[][] {
// r,
{ 0.5, 0.0, 0.0, 0.5, 0.0, 0.0 },
{ 0.5, 0.0, 0.0, 0.5, 0.5, 0.0 },
{ 0.5, 0.0, 0.0, 0.5, 0.0, 0.5 } }, new double[] { 0.3333,
0.3333, 0.3334 }));
- Adapt a colour palette to the rendering of your images and make optimum use of the panel through the distance and offset parameters. Impressive results from last year's ICS4U ACES can be viewed here...


 LINDENMAYER
SYSTEMS.
With Koch Constructions and the concept of fractal dimension as a foundation,
we can now take one step closer to our goal of rendering of natural forms.
Not surprisingly, credit for this stage goes to a Hungarian biologist/botanist, Aristid
Lindenmayer,
who, in 1968, introduced a formalism associated with the expression of plant
structures, known today as L-Systems. The grammar embodied within
L-Systems lends itself readily to computer graphic rendering.
LINDENMAYER
SYSTEMS.
With Koch Constructions and the concept of fractal dimension as a foundation,
we can now take one step closer to our goal of rendering of natural forms.
Not surprisingly, credit for this stage goes to a Hungarian biologist/botanist, Aristid
Lindenmayer,
who, in 1968, introduced a formalism associated with the expression of plant
structures, known today as L-Systems. The grammar embodied within
L-Systems lends itself readily to computer graphic rendering.
An electronic copy of a wonderful text on the subject of Lindenmayer Systems,
entitled The Algorithmic Beauty of Plants (ABOP) is available for
download by following the image link to the left. The related Algorithmic
Botany website offers
additional inspiration.
The algorithm
for generating these
images
is
defined by an initiator (axiom) and
one or more generators (productions) used to propagate
the shape over successive generations. In this assignment, we'll use
a string for
the axiom and a set of production mappings to define
the image. A recursive generation algorithm coupled with a character replacement
strategy of your choice (see String methods)
by their production mappings grows the
image. Finally each generation is drawn with a virtual pen (similar
to a plotting device) on a JPanel in response to characters in the encoded
String. Here is a table containing some of the images you'll be rendering,
together with some original curves developed by former ACES. See Framework.html to view the animated renderings.
Task.
 Add a new menu to the immediate right of Koch,
entitled Lindenmayer.
Add a new menu to the immediate right of Koch,
entitled Lindenmayer.- Under the Lindenmayer menu,
add the same menu items that appear in
Framework.html. Consult pages 8-10 of the ABOP handout for details of the Koch Snowflake,
the Koch
Island and Figures 1.7, 1.8, and 1.9 onward.
- Create a new Activity class
with the name of LSystem (LSystem
documentation).
The animation strategy will be to render the image as a plotting device
would,
one segment at a time. Here's an example of an instantiation: Figure 1.7 with Code.
- Create a Turtle class that
encapsulates the properties of the drawing pen manipulated by LSystem's draw() method
(Turtle documentation).
- (Optional) Feel free to incude an L-System of your own design/creation or
even one you've googled. Alternatively, how about an origami
version?
- Submit your updated Catalog source
code to handin

 KOCH
CONSTRUCTIONS: Triadic Koch Snowflake and Quadratic Koch Island.
With a preliminary understanding of the Cantor Set we
are ready to undertake a related set of
fascinating structures attributed to Helmut Koch
that continued to challenge the conventional notion of dimension well
into the 20th Century. Whereas Cantor appeared content to simply remove the middle third of
a line
segment, Koch proposed that it be replaced by two segments of equal length.
KOCH
CONSTRUCTIONS: Triadic Koch Snowflake and Quadratic Koch Island.
With a preliminary understanding of the Cantor Set we
are ready to undertake a related set of
fascinating structures attributed to Helmut Koch
that continued to challenge the conventional notion of dimension well
into the 20th Century. Whereas Cantor appeared content to simply remove the middle third of
a line
segment, Koch proposed that it be replaced by two segments of equal length.
The bridge from Cantor to Koch can be inferred from the graphic below left
that also suggests the recursive application
of each strategy. Koch went further. Using each of the three sides of an equilateral
triangle as initiators he applied his replacement strategy
(generator) repeatedly, to produce the perimeter of his classic Koch Snowflake below
right.
Now it gets really interesting. Koch's replacement proposal opened
the door to a variety of generators, one of which led to the Quadratic
Koch Island depicted below.
The iconic Triadic Koch Snowflake and Quadratic
Koch Island belong to the set of Space-filling
curves or Sfcs (Pfcs for now). The realization of
this assignment will result in the next menu in your Catalog devoted to a class of Sfcs that we'll attribute to Koch (there's
not enough time in this course to investigate 3D Sfcs (Hilbert Cube) but I'd welcome an email from you someday linking me to
your future explorations).
Task.
-
-
Add a new Koch menu to your Catalog project, to the right of Cantor as shown below,
-
Create a new Activity class
by the name of TriadicKoch that encapsulates an ArrayList<Sprite> of
size equal to the maximum depth of generation.
-
A call to
Sprite's
createData() method
(or some similar call) can create an equilateral triangle as
a generation 0 starting point. Subsequently it can be rotated
and scaled into position through appropriate Matrix2D transformation calls.
-
Using an algorithm similar to the textbook example above, employ recursive
generation strategy to
propagate a sequence of Sprite objects representing the outline of successive
generations of the Koch Snowflake.
-
Koch's draw(BufferedImage
img) method can
create and fill a Polygon from the respective Sprite data.
-
Repeat the 4 steps above for the class QuadraticKoch.
-
(Optional) Design your own generator, implement it, name it, and add it
to your menu.
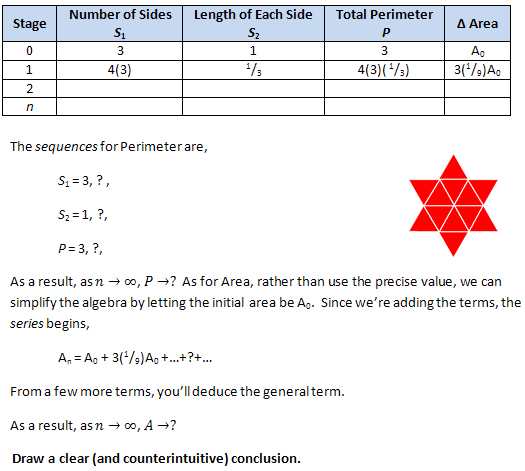
 CANTOR
SETS (Part 3 of 3): Triadic and Quadric Cantor Strategies. Look
at the gif animations below. Execute Framework.jar to see them live. Your
previous experience with the Linear Cantor
Set would
suggest that a recursive removal algorithm could be undertaken to generate
these 2D Cantor Sets as well. Although we don't have the time to pursue an
investigation of the 3D Cantor Set this
year, it may be something you may wish to investigate in the future.
CANTOR
SETS (Part 3 of 3): Triadic and Quadric Cantor Strategies. Look
at the gif animations below. Execute Framework.jar to see them live. Your
previous experience with the Linear Cantor
Set would
suggest that a recursive removal algorithm could be undertaken to generate
these 2D Cantor Sets as well. Although we don't have the time to pursue an
investigation of the 3D Cantor Set this
year, it may be something you may wish to investigate in the future.
Task.
- Under the Cantor Sets menu,
and another item entitled, Triadic.
- Implement a new Activity class
entitled TriadicCantor.
Its constructor should receive the maximum depth of removal. The
animated gif (above left) presents a depth of 7. Your constructor should
generate a entire collection of subsets to be 'removed' prior to finishing.
In this way the draw() method
will simply access the require number of levels on each call.
- Repeat Steps 2 and 3 by implementing the class QuadricCantor.
- A premium will be reserved for code that is efficient, clear and well documented.
One of the ways this can be accomplished is to make maximum use of the Polygon class
and any of the JCF data structures we've studied.
- The original triangle has an area. With each recursive stage, area is removed.
Two interesting
questions
to
ask yourself then is, "How
much area remains at each stage of the deconstruction?", and "Eventually,
is all the area removed or is there a limit?". After a few weeks
of Calculus you'll be able to formulate a mathematical answer to these questions.
Let me know when you get there and we'll discuss it.
 CANTOR
TERNARY SET (Part 2 of 3): Implementation
CANTOR
TERNARY SET (Part 2 of 3): Implementation. A gasket-like object can be constructed by a process that removes parts of its body. In this assignment
you are asked to render the Linear Cantor Set with a strategy involving
rectangles of minimal height to represent
the
line segment intervals.
 Complete this Cantor Set investigation with pencil & paper. (Word, PDF)
Complete this Cantor Set investigation with pencil & paper. (Word, PDF)- Add the menu structure defined by the screen capture in Class 53 to your Catalog (Framework) project.
- Implement a new Activity (Drawable) class
entitled LinearCantor.
Its constructor should receive the maximum depth, n, of removal.
The animated gif to the right presents a depth of 5.
- Since the total number of segments can be determined beforehand from the depth, the constructor can instantiate a collection of predetermined size to house all the segments. The collection is to be fully populated before the constructor ends through a call to the recursive method propagate(Point2D segment, int d) where segment is the original length and d is 1 (just as we have a number of times before, the collection's data will be used to support an animation by your draw method).
- Display the Cantor Set to depth of at least 5 generations.
- A premium will be reserved for code that is efficient, clear, and well documented.
Feel free to execute this version of Framework.jar to see the results for this and the future Cantor fractals.
 CANTOR (TERNARY) SET (Part 1 of 3): Analysis
CANTOR (TERNARY) SET (Part 1 of 3): Analysis. The
Cantor
Set is an appropriate launch point for our consideration of fractal
and topological dimension. A recursive (or iterative) algorithm removes an
open third of each segment at each stage of propagation. For this reason,
the Cantor Set is also known as the
ternary or
middle third Set.
Here is a link to Wolfram's
(Mathematica) animation of the
Cantor Set and the
Cantor Function.

- You are asked to research the Cantor Set using as many references
as you require to explain the propagation process in your own
words
and identify one or more of its remarkable properties.
- The table below presets a quantitative analysis
of the stages of the Cantor propagation. Based on your research be able to explain the table to the class when asked.
- State the Fractal (Hausdorff) dimension of the Cantor Set accompanied
by an explanation.

-
The original line segment has a length. With each recursive stage,
length is removed. The interesting question
to ask yourself then is, "Eventually, is all the length removed?"
 Catalog: Calculus
Catalog: Calculus. This submission will require a merge of your two major projects this year. The two projects will continue to cooperate with one another over the course of the year but as remain in separate entities. For guidance, refer to the
2011 ICS4U Final Exam.
Task.
- Be sure to have added your Calculus Project to the Build Path of your Catalog Project.
- Add a new top-level menu, entitled Calculus with submenus as shown.
- Selecting the Enter f(x)... submenu item, launches a dialox box that allows the user to submit a function definition. Be sure to offer a default definition.
- Selecting the Graph submenu item without a valid function entry, results in the display of an error dialog box, otherwise the graph of the function, over a suitably square domain and range, is displayed. You may wish to review the Model and View design decisions in last year's Parametric Equations Project.
Submit documented source code by Sunday February 8 as instructed.

 Elective. (Status: OPEN) The first ACE to commit to this Project in an email to me can use a successful implementation of this task to improve his mark on either a previous or future assignment. (Programmer: ??. Start: ??. Finish: ??)
Elective. (Status: OPEN) The first ACE to commit to this Project in an email to me can use a successful implementation of this task to improve his mark on either a previous or future assignment. (Programmer: ??. Start: ??. Finish: ??)
CBC Logo. CBC logos have changed over the years. Its current kaleidoscopic image offers the analytical mind of a curious ACE the chance to explore a recursive deconstruction of the circle.
One analysis suggests the core of the image to be a simple red circle. Compass-direction based sliced partitions of the circle then appear to animate outward, proportionally, at which point a secondary partition is undertaken and the animation extends to a second level.
Task.
- Perform your own analysis of the logo animation.
- Add a CBC Logo menu item within the Studies menu of your Catalog project and implement an Activity-based CBCLogo class.
- Starting with a circle (Ellipse2D.Double) object as the core, design and implement a recursive geometric strategy to deconstruct the object into, say, 'tiles'.
- The tiles can be used as the bases for Area objects that can be assembled into a Collection.
- The presentation of the collection can then be supported through strategic use of AffineTransforms embedded within a threaded execution.
- One month will be allotted from the date of commitment to submit exemplary, working Catalog source code and, if you can, your animated gif, CBCLogo.gif.
 Elective. (Status: OPEN) The first ACE to commit to this Project in an email to me can use a successful implementation of this task to improve his mark on either a previous or future assignment. (Programmer: ??. Start: ??. Finish: ??)
Elective. (Status: OPEN) The first ACE to commit to this Project in an email to me can use a successful implementation of this task to improve his mark on either a previous or future assignment. (Programmer: ??. Start: ??. Finish: ??)
Combination Lock I. Since Java's LinkedList<E> class
maintains this data structure as a doubly-linked list, users can
traverse it forward and backward with the help of a ListIterator<E> object.
Create the project LockTest and a driver that manipulates
the class, Lock,
defined by the UML specification below. You will need to complete the conditions
in each of the while statements in the driver for the project to work correctly.
A correct implementation of the Lock class instantiated with
the combination 21-32-34, will generate the following output,
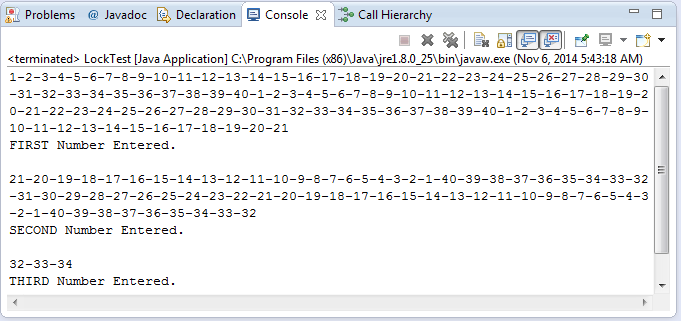
 Combination Lock II. Visualization of Combination Entry. The goal of Part II of the Combination Lock project is to present an accurate rotation of the dial of your Dudley lock as required for any user-requested combination.
Combination Lock II. Visualization of Combination Entry. The goal of Part II of the Combination Lock project is to present an accurate rotation of the dial of your Dudley lock as required for any user-requested combination.
In the animation above right aI single clockwise rotation of the dial is presented to give you an idea of the semi-realistic outcome you're aiming to achieve. To accomplish this, I downloaded an image of the Dudley lock (below) and cut out the dial only as a square with a transparent background (right).
With the background BufferedImage of the lock drawn first, the draw() method of the Activity can apply a sequence of 1° rotations (AffineTransformation) to the dial before drawing over top of the background.
Task.
- Add the Lock class, unaltered from the LockTest project in Part I to your Catalog project.
- Add Combination Lock as a new menu item within your Studies menu.
- Create a CombinationLock class as a new Activity, within your Catalog project.
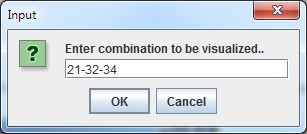
- Selection of the Combination Lock activity should result in a request for the user to submit a combination for execution, similar to the dialog to the right.
- The Combination Lock object is mounted on a Thread and run as an animation until the combination is displayed and the lock appears opened!
- One month will be allotted from the date of commitment to submit exemplary, working Catalog source code and, if you can, your animated gif, DudleyLock.gif.
 Calculus Project: Expression 'Language'.
Of all the assignments you've been asked to complete over the past couple of years,
you'll likely remember this as one of the most satisfying. As could be expected of a comprehensive project, it attempts to tie together some of the most important concepts within the co-disciplines of mathematics and computer science. For years to come,
you will
marvel at what you are about to accomplish. Finally, since your exam will expect that you extend this work in some new direction, you are encouraged to develop efficient and well-documented code.
Calculus Project: Expression 'Language'.
Of all the assignments you've been asked to complete over the past couple of years,
you'll likely remember this as one of the most satisfying. As could be expected of a comprehensive project, it attempts to tie together some of the most important concepts within the co-disciplines of mathematics and computer science. For years to come,
you will
marvel at what you are about to accomplish. Finally, since your exam will expect that you extend this work in some new direction, you are encouraged to develop efficient and well-documented code.
The first step in writing IMAGE-Algebra&Geometry many years ago
was a three-month investment in developing a
customized language before
an
interpreter could be undertaken. At the root of every language there are a set of tokens (vocabulary) upon which is based a set of rules for assembling the tokens (grammar). Similarly, your first step in developing an application to manipulate
mathematical expressions is to develop an unambiguous language for the
expressions
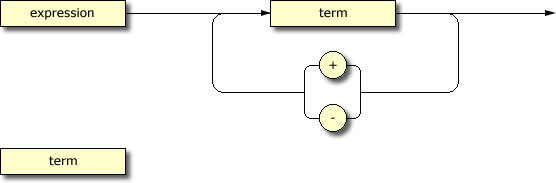
you expect to interpret. There are different ways to define grammars. The eXtensible Markup Language (XML) is in widespread use today. Backus Naur Form (BNF) is common within the computer science community (Example: ASCIIMathML Syntax). We'll use the intuitive 'railway diagram' strategy.
Based on your understanding of secondary school level mathematical expressions, reduce the terminology into a vocabulary (consider these) and, from there, engineer a recursive grammar by completing an unambiguous sequence
of railway diagrams that will embrace the broadest range of mathematical
expressions you have encountered to this point. Here's how
your grammar will begin...
 Matrix2D
Enhancements
Matrix2D
Enhancements. Important enhancements to your
Matrix2D class
are required to support future investigations of the
Collage
Theorem and, ultimately,
IFS Codes. These include
the concepts of the
determinant and
inverse of a matrix and their application to solving systems of equations.
-
Implement the above definition through the method
public
double getDeterminant() to be added to your
Matrix2D class.
Generalize your design so that the determinant of a square matrix of
any dimension could be found using the supporting methods highlighted
in red in the Explorer view below (
coFactor,
determinant, and
minor).
Add statements at the end of
your
Matrix2DTest driver to confirm
your results.
Here's a worked
example to assist with your development.
Add the driver DeterminantTest.java to your Animation2D project to yield results similar to this. This will require you implement the DAY 1 methods below.
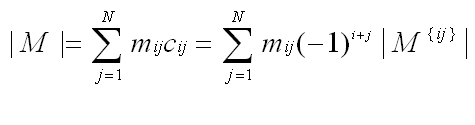
-
To make things clearer, I've colour-coded
an Explorer view of the methods that need to be implemented at each stage of the project.
-
(
DAY
2)
 Cramer's Rule.
Cramer's Rule.
 One method for solving a relatively simple system
of n equations with as many unknowns acknowledges Gabriel
Cramer (1704-1752)
for a computationally-friendly algorithm. Here's a description,
One method for solving a relatively simple system
of n equations with as many unknowns acknowledges Gabriel
Cramer (1704-1752)
for a computationally-friendly algorithm. Here's a description,
- Consider a system
represented in the matrix form, Ax=b,
where A is the n × n coefficient matrix, x is
the variable column vector with n elements and b is the right-side
column vector with n elements.
- Let Ac be the matrix obtained by replacing column c with b.
- Let the determinant of A be represented as D.
- Let the determinant of Ac be represented as Dc
- Cramer's Rule defines the solution to the system as,

where D ≠ 0.
-
Add the method
public double [] cramersRule( double
[] b
) to your Matrix2D class
that returns the solution x to the system Ax=b
, where A is this Matrix2D object.
You are to make maximum use of existing Matrix2D resources
and keep the rest
of your code as tight and efficient as possible. Add a call to Matrix2D's solveSytem method (it will simply call cramersRule for
now) statements
at
the
end
of
your Matrix2DTest driver to solve and display the solution to the system in i. above.
-
(
DAY 3)
 The Inverse
of a Matrix.
The Inverse
of a Matrix. Just as a (multiplicative) inverse exists for
all real numbers,
x, (except 0), so, too, does the inverse of a
square matrix
A (det
A≠0). The inverse of
A can
be defined as,
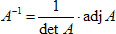
where
adj A is the
adjoint of
A.
The
adjoint of A is the matrix obtained by transposing the matrix of cofactors
of
A.
Implement the
blue
DAY 3
methods above, as follows,
- the transpose() method reflects
the element in the main diagonal. That is, the element at row r, column c is
exchanged with the element at row c, column r. NOTE. This
would be a perfect opportunity to practice the technique of swapping
elements without the use of a third variable.
- the scalarMultiple(double k) method
simply multiplys each element of the matrix by the scalar parameter.
- the adjoint() method simply
returns a new Matrix2D object
populated with the coFactors of A that have been transposed.
- if the previous 3 methods are implemented as recommended, the inverse() method
can return its result in a single expression as follows,
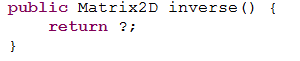
Add statements to your Matrix2DTest
driver to test your inverse() method (make
sure to check that the determinant is not 0 beforehand!)
-
(
DAY 4)
 Elective. (Status: OPEN) The first ACE to commit to this Project in an email to me can use a successful implementation of this task to improve his mark on either a previous or future assignment
Elective. (Status: OPEN) The first ACE to commit to this Project in an email to me can use a successful implementation of this task to improve his mark on either a previous or future assignment.
(Programmer: ??. Start: ??. Finish: ??)
Gauss-Seidel. An interesting iterative strategy for solving a system of equations is referred to as the
Gauss-Seidel method. Essentially, one simply picks a
random solution and, through a repetitive feedback process, the output converges to the solution (
under certain circumstances).
Task.
- Research the Gauss-Seidel technique for solving systems of equations.
- Add methods to your Matrix2D class that enables users to efficiently exploit the Gauss-Seidel technique for solving a system of 3 equations in three unknowns.
- Add statements to your Matrix2DTest driver class to exercise your enhancements.
- Prepare instructional material on the technique and be prepared to teach it to your classmates.
- One month will be allotted from the date of commitment to submit exemplary, working source code.
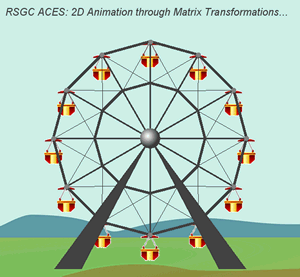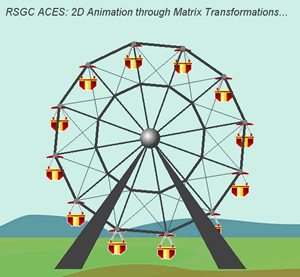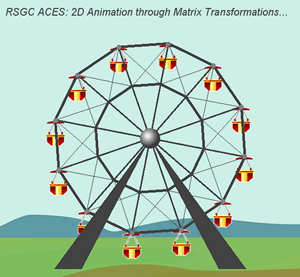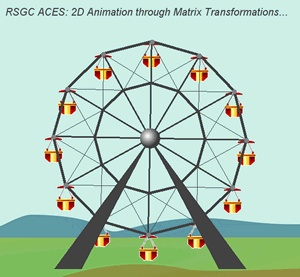
 Animation2D: Part 3. Animation2D. In
this final instalment, we integrate the foundation classes
you have developed over the previous two projects to demonstrate the applicability
of matrix-defined transformations to simple, but compelling, two-dimensional
animations. In the example below, a subject was sourced on the internet and an approximation developed with the tools developed in previous exercises that required the use of all four affine transformations (rotation, reflection, scaling and translation).
Animation2D: Part 3. Animation2D. In
this final instalment, we integrate the foundation classes
you have developed over the previous two projects to demonstrate the applicability
of matrix-defined transformations to simple, but compelling, two-dimensional
animations. In the example below, a subject was sourced on the internet and an approximation developed with the tools developed in previous exercises that required the use of all four affine transformations (rotation, reflection, scaling and translation).
With your Matrix2D and Transform2D tools in place, you are ready to implement an animation based on matrix transformations, built on transformations. Before you do, let's look at the way previous ACES undertook the project in recent years. Add this driver to your Catalog Project and
review and execute the code. The general idea is to transform one or more Sprite objects to the coordinates for the next frame within the updateScene() method.
The loop in the run() method called the paintPanel() method
in which you can retrieve your Sprite's updated coordinates to populate a Polygon object.
This polygon object can be added to the scene through a call to Graphic2D's draw() method. Here's
the full Javadoc. Considering your vast
exposure to gaming animation, I know you'll take your effort
to a whole new
level.
Task.
- Identify a scene you'd like to animate and contribute to our ICS4U animation archive. Credit for this project will reflect both the creativity of the scene and its execution.
- Decide on a name for the animation and add a new item in the Studies menu under RPN Evaluator. Create a new class by this name as an extension of the Activity class.
- Given that you have successfully loaded images for the previous Puzzle activity, acquire a gif image that will serve as a background for your animation. It must be a gif (or PNG 8) file format because a standalone animated gif of your animation will be created and graphic formats requiring more than 256 colors will not render attractively.
- Draw Sprite objects are back to front, ensuring the scene contains both background and foreground objects, with the former eclipsing the latter.
- The classes
in this project reflect a strong hierarchical design. I would expect your
code to capitalize on the strength
of this design; writing clean, tight, efficient carefully-crafted statements that
fully exploit the cascading nature of the respective class methods.
- Once your animation is ready to go, use your ability to capture frames to save a sequence of gif images to disk using your saveImage(bi) method. The filenames of your gif images must be of the form: xxxxddd.gif where x can be any character and the ddd is a sequence of digits with leading 0s. These are to be attached to your submission.
- Creative. Processing's Movie Maker feature can be used to assemble a sequence of images into a movie (.mov). Once again, use your ability to capture frames to save a sequence of images to disk using your saveImage(bi) method. Source a generic audio file as a soundtrack. Attach the .mov file to your submission.
Submission. Attach documented source files for your entire Catalog project, the .gif files for the animation and your .mov file,
to an email to handin with the Subject: Animation2D by
the deadline.
 Animation2D: Part 2. Transform2D
Animation2D: Part 2. Transform2D. In the second
instalment of the
Animation2D project, you will explore matrix-based transformations in R
2.
Task.
- Add the driver, Transform2DTest.java. to your Catalog project
and review the code.
- Also, add the class file Point2DList.java and
review this code.
- Write the two class files, Transform2D.java and Point2D.java,
that will work seamlessly with the other existing classes to produce this
output. I have prepared the documentation that
will guide your effort.
 Animation2D: Part 1. Matrix2D. In this 3-part project you are introduced to the matrix algebra of transformational
geometry
leading
to
a creative graphic animation. Below are the submissions of this year's ACES.
Check out more samples from ACES of previous years:
Animation2D: Part 1. Matrix2D. In this 3-part project you are introduced to the matrix algebra of transformational
geometry
leading
to
a creative graphic animation. Below are the submissions of this year's ACES.
Check out more samples from ACES of previous years:
Task.
- Add the driver Matrix2DTest.java to your Catalog Project.
- Making every attempt to maximize the
use of a minimal set
of methods, develop a set of cascading set of constructors and required methods
for the class Matrix2D that
can be used with the driver Matrix2DTest.java to
produce this
output.
- Minimize the dependency of your code on direct reference
to the only instance field, matrix.
- At all stages be aware of the implications of deep vs shallow object references. Careless coding in this regard can lead to bugs that are difficult to detect and time-consuming to repair.

 Reverse Polish Notation (RPN) Evaluator. The next enhancement to your Catalog catalog requires the application of your recursive skills to the evaluation of arithmetic expressions expressed in postfix (operators follow their operands) rather than the common infix form we are accustomed to. The animated gif to the right demonstrates the evaluation of the postfix expression, 235*+.
Reverse Polish Notation (RPN) Evaluator. The next enhancement to your Catalog catalog requires the application of your recursive skills to the evaluation of arithmetic expressions expressed in postfix (operators follow their operands) rather than the common infix form we are accustomed to. The animated gif to the right demonstrates the evaluation of the postfix expression, 235*+.
To assist with the evaluation, you will maintain a Stack<Integer> to track your progress. The end result of the project will be to animate the collection of intermediate Stack<Integer> objects to offer the viewer a frame-by-frame animation of the stack sequence
Task.
- Add a new Activity class to your Catalog project by the name of RPNEvaluator and add an RPN Evaluator menu item within the Studies menu.
- On launch, offer a JOptionPane dialog box to your users containing a default postfix expression for evaluation that they can edit if they wish.
- The evaluation of the postfix expression will be initiated and completed within the RPNEvaluator's constructor with the help of strategic helper methods including the recursive: private void evaluate(int c) method that uses the explicit parameter c as a cursor it advances through the expression. As it processes the expression, it manipulates a Stack<Integer> object, pushing and popping Integer operands as required. Hint: the Character class has an isDigit(char ch) method. All changes to this Stack<Integer> are to be recorded in the larger collection for final animated playback through RPN Evaluator's draw() method.
- Effective presentation of the sequence is key. The contents of the stack should be centered horizontally, and should grow from the bottom of the panel, upwards. This will take some thought. Make the optimum use of the height of the panel. Experience in working with the Font class within your About panel will prove useful. Be sure to activate antialiasing.
- For simplicity, assume each operand in the initial expression is a single-digit integer.
- In this, as with all projects, use your knowledge of Big O behaviour to make the best data design decisions.
- In this, as with all projects, use your knowledge of iteration and Iterator<E> alternatives to make the best code design decisions.
- Develop, document, and submit all Catalog files by the deadline.
 Elective. (Status: CLOSED) The first ACE to commit to this Project in an email to me can use a successful implementation of this task to improve his mark on either a previous or future assignment. (Programmer: SB. Start: November 23. Finish: January 25)
Elective. (Status: CLOSED) The first ACE to commit to this Project in an email to me can use a successful implementation of this task to improve his mark on either a previous or future assignment. (Programmer: SB. Start: November 23. Finish: January 25)
Sudoku. One of the most popular pastimes TTC riders engage in is solving a Sudoku puzzle. Since your recursive skills are rapidly improving, wouldn't it be a crowning achievement to code a Sudoku-solver? An animated gif of my row-major solution appears below right (similar to the technique introduced last year to demonstrate the sorting algorithms). The first few thousand images (4209 in total) develop the solution slowly (giving you an opportunity to witness the backtracking you'd expect from trial and error) but, as you'd suspect from an algorithm with exponential Big-O, it finishes up pretty quickly.
Task.
-
Add an Activity class to your Catalog by the name of Sudoku. This class encapsulates a starting model of the Sudoku game to right, as in,
byte [][] model = {{5,3,0,0,7,0,0,0,0},{6,0,0,...
where 0's are used to represent empty places in the board.
- Since the goal is to animate
your presentation after the recursive solution is discovered, you'll need a data structure to hold the frames, as in,
ArrayList <byte[][]> solution;
- Your Sudoku constructor should add the starting model to the solution list prior to calling your recursive solver method, solve(x,y), where (x,y) starts at (0,0).
- To keep the solve(int x,int y) method as lean as possible, I suggest the inclusion of some supportive helper methods, similar to,
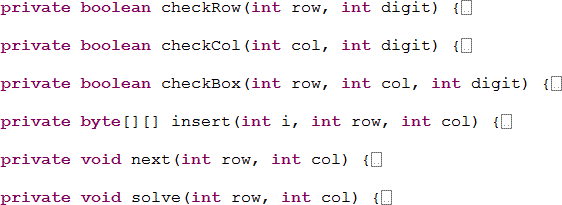
-
For the recursive solve(int x,int y) method, the basis condition and inductive stages must be determined. For the former, it should be appreciated that the puzzle would be solved if 9 rows were correct. For the inductive segment, it should be realized that for unfilled entries (0) the potential for all ten digits being inserted must be enabled to ensure that the existing row, column and Box entries to that point are unique. New insertions should trigger a saving of the model for later replay. If a repetition is found, the cell entry should be set back to 0 and backtracking should occur.
-
Once the puzzle is solved, the draw() method can simply replay the saved frames from solution.
-
One month will be allotted from the date of commitment to submit exemplary, working Catalog source code and, if you can, the animated gif, Sudoku.gif.
 Brackets. The example
method on page 480 offers an iterative solution to confirm whether a String consists of correctly matched parentheses. It would be more impressive if
it were recursive.
Brackets. The example
method on page 480 offers an iterative solution to confirm whether a String consists of correctly matched parentheses. It would be more impressive if
it were recursive.
Task.
- Create a project called BracketTest and
drop in this driver.
- The class contains an instance field of type, Stack<Character> that
can be exploited from within the recursive matchParens(String
expr, int i) method.
- The predicate methods, isOpenBracket(char
ch) and isCloseBracket(char
ch) are to be used to write cleaner, more readable code within your matchParens method.
- Output should appear as follows,
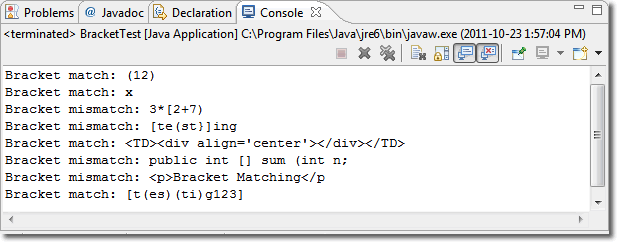
 Elective. (Status: OPEN) The first ACE to commit to this Project in an email to me can use a successful implementation of this task to improve his mark on either a previous or future assignment. (Programmer: ??. Start: ??. Finish: ??)
Elective. (Status: OPEN) The first ACE to commit to this Project in an email to me can use a successful implementation of this task to improve his mark on either a previous or future assignment. (Programmer: ??. Start: ??. Finish: ??)
Puzzle 3. Sliding Tiles. I'm somewhat reluctant to offer this Project because it is difficult and success can be elusive. On the other hand, underestimating the talent and motivation of my ACES has never proven wise. So, accept the challenge at your own peril and know, beforehand, that my successful pursuit robbed me of no less than four hours of enjoyment of a sunny and warm October Saturday afternoon. The first five moves of one session has been captured in the animated gif to the right.
Task. Modify Puzzle2 to yield tiles that slide into the adjacent blank slot when clicked, reflecting a more realistic representation of the mechanics of the actual puzzle.
Note. The sliding interval in the animation to the right is longer than the one I set in for the creation of the gif. It must have something to do with browser-specific settings...

 Elective. (Status: CLOSED) The first ACE to commit to this Project in an email to me can use a successful implementation of this task to improve his mark on either a previous or future assignment. (Programmer:
Elective. (Status: CLOSED) The first ACE to commit to this Project in an email to me can use a successful implementation of this task to improve his mark on either a previous or future assignment. (Programmer:  . Start: October 22. Finish: December 31)
. Start: October 22. Finish: December 31)
Fibonacci Spiral. Review Wikipedia's description of the Fibonacci spiral which approximates the Golden spiral.
Task.
- Embed within your Catalog Project a new Activity class entitled, FibonacciSpiral.
- The animation produces three outcomes: a linear sweep arm, the adjoining squares of the Fibonacci sequence (dimensioned from the numbers and filled, modularly, from a 5-colour palette) and a single GeneralPath object that connects the inscribed quarter arcs of each square to yield the spiral.
- One month will be allotted from the date of commitment to submit exemplary, working Catalog source code and, if you can, the animated gif, FibonacciSpiral.gif.
 Catalog: File Menu: Open | Exit
Catalog: File Menu: Open | Exit. For this weekend's
Puzzle2 segment you may prefer to open images for puzzling other than the latest image in
Content panel. These can be images you have previously generated and saved, or from some other source altogether.
Add the File Menu as it appears to the right. Add the Catalog field,
private static File file;
In your actionPerformed (ActionEvent ev)
handler add the following code,
if ("Open".equals(command)) {
try {
if (openImage() == JFileChooser.APPROVE_OPTION) {
content.current = new LoadImage(file);
content.createNewImage();
content.repaint();
}
} catch (FileNotFoundException e) {
// TODO Auto-generated catch block
e.printStackTrace();
}
}
else if ("Exit".equals(command)) {
dispose();
System.exit(0); // calling the method is a must
}...
The Open command requires the following supporting method,
private int openImage() throws FileNotFoundException {
String filePath = new File("").getAbsolutePath();
JFileChooser chooser = new JFileChooser(filePath);
FileNameExtensionFilter filter = new FileNameExtensionFilter(
"Catalog Files", "png");
chooser.setFileFilter(filter);
int returnVal = chooser.showOpenDialog(this);
if (returnVal == JFileChooser.APPROVE_OPTION) {
file = chooser.getSelectedFile();
} else
System.out.println("Open cancelled.");
return returnVal;
}
Finally, add this class,
public class LoadImage extends Activity {
File file;
public LoadImage(File file) {
super(Color.black, Color.white, "LoadImage");
this.file = file;
}
public void draw(BufferedImage bi) {
super.draw(bi);
Graphics2D g2D = (Graphics2D) bi.createGraphics();
BufferedImage img = null;
try {
img = ImageIO.read(new File(file.getName()));
} catch (IOException e) {
}
g2D.drawImage(img, 0, 0, null);
}
}
 Catalog: Cosmetic Enhancement
Catalog: Cosmetic Enhancements.
Centering. A convenience for your users is to have your application appear in the center of the screen at launch. Study and add the following method to your Catalog class and a call from the constructor if you wish.
private void centerFrame() {
// Center the JFrame on the screen...
GraphicsConfiguration gc = getGraphicsConfiguration();
Rectangle rect = gc.getBounds();
setLocation((rect.width - appDimen.width) / 2,
(rect.height - appDimen.height) / 2);
}
Gradient Fills. In the screen capture to the right I designed and applied a simple Gradient Fill to the background of my About panel. The code I used appears below,
Rectangle bounds = new Rectangle(0, 0, width, height);
Point2D start = new Point2D.Float(0, 0);
Point2D end = new Point2D.Float(bounds.width, bounds.height);
float[] dist = { 0.0f, 0.3f, 1.0f };
Color[] colors = { Color.RED, Color.WHITE, Color.BLUE };
LinearGradientPaint p = new LinearGradientPaint(start, end, dist,
colors);
g.setPaint(p);
g.fill(bounds);
Antialiasing. Compare the quality of the text in the two About panels below. The one on the right had antialiasing enabled with the statement below,
g.setRenderingHint(RenderingHints.KEY_TEXT_ANTIALIASING,
RenderingHints.VALUE_TEXT_ANTIALIAS_ON);
Try your hand at the game.
Part 1. Mathematical Underpinning: Permutations and Parity. The object of the puzzle is to slide a random permutation of the tiles into the proper sequence moving one tile at a time.
- Consider a 4-puzzle arranged as a 2×2 square with the last tile removed and the remaining three randomly placed. Question. Will all possible permutations of the first three squares enable the player to 'solve' the puzzle?
- Look deeper into the underlying mathematics at Cut The Knot.
Additional Reference:  Taxicab
(Manhattan) Distance
Taxicab
(Manhattan) Distance
Since not all randomly-generated permutations are solvable the designer has a challenge. A random, brute-force strategy would be to perform some minimum number of tile swaps, stopping at the first one after which is deemed solvable. Alternatively, a deterministic algorithm would perform a predetermined number of swaps in which the empty square trades places with an immediate neighbour. In this way, no matter how many swaps are made, the puzzle is always solvable (simply by reversing the sequence of swaps).
Task.
 Add a Puzzle menu item to the Studies menu of your Catalog project.
Add a Puzzle menu item to the Studies menu of your Catalog project.- Implement the Puzzle class according to the UML outline to the right. The Puzzle constructor accepts cap, the most recent BufferedImage that currently appears on the Content panel; dim, the side dimension of tile matrix (4 for the 15 puzzle) and numFrames, the number of frames in the animation (it was agreed that `dim^3` would result in reasonable coverage of the matrix.
- Strategic elements of the algorithm were developed together in class as a group.
- Selecting Puzzle option from the Studies menu should launch the user directly into the 15 puzzle (4×4). It was agreed upon in class that an animated view of tiles being randomized led to a preferred user experience. To accomplish this, it is recommended that the Puzzle constructor should instantiate the frames matrix (array of arrays) to numFrames rows. Each row is then populated with a new map array that reflects the order of the tiles after each swap. In this way, when the draw() method is eventually invoked on a thead, it can simple 'play' the frames matrix, one row at a time so the user can view an animation of the blank tile moving about.
Possible Part 1 Enhancements include,
- A JOptionPane dialog that allows the user to determine the dimension.
- A JOptionFileChooser dialog that allows users to load a graphic file to be puzzlized.
- Smooth slide animations of the tiles.
 Puzzle 2. Solution. The animation below left simulates the slides an average player might undertake in solving the puzzle.
Puzzle 2. Solution. The animation below left simulates the slides an average player might undertake in solving the puzzle.
Task.
 Being the highest level class in the application, the Catalog class is best suited to listen for mouse events and pass control to the active panel class. Enhance the Catalog class signature as follows,
Being the highest level class in the application, the Catalog class is best suited to listen for mouse events and pass control to the active panel class. Enhance the Catalog class signature as follows,
public class Catalog extends JFrame implements
ActionListener, MouseListener {
- As can be determined from the documentation of the MouseListener interface, there are five methods that must be appear in a successful implementation.
- To register your Catalog object for mouse event notifications from the OS, it is necessary to add the following statement to your Catalog constructor,
this.addMouseListener(this);
- Since many of the activities this year will benefit from mouse interactivity, it would be wise to add a
public void handleMouseLocation(int col, int row)
method to your Activity class (see UML above, right) with the expectation that subclasses that require the support override the method.
- For this activity, you might consider adding a body only to,
public void mouseClicked(MouseEvent me)
The MouseEvent object received will include the absolute screen coordinates of the mouse icon's hot point. Before calling current's handleMouseLocation method, you should convert to relative coordinates. To accomplish this you need to determine the insets defined by the JFrame. Add the following statements to your Catalog class,
private static Insets insets;
and
insets = frame.getInsets();
With this data, you can convert to relative mouse coordinates. before passing them to handleMouseLocation.
- To identify which Activity object current references, you can employ the instanceof operator.
 Elective. (Status: CLOSED) The first ACE to commit to this Project in an email to me can use a successful implementation of this task to improve his mark on either a previous or future assignment. (Programmer: RS. Start: September 29. Finish: October 29)
Elective. (Status: CLOSED) The first ACE to commit to this Project in an email to me can use a successful implementation of this task to improve his mark on either a previous or future assignment. (Programmer: RS. Start: September 29. Finish: October 29)
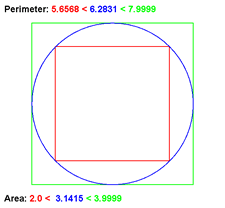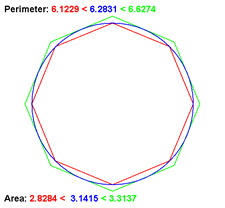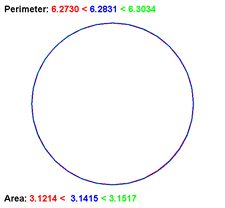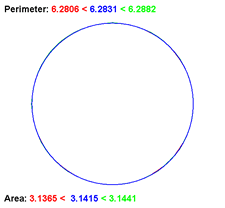 Antiphon's Process of Exhaustion. Calculus' central concept is the notion of a limit. This project conveys the idea of a limit through geometric animation. Antiphon (5th Century BC) is credited with the demonstrating that if the number of sides of a regular polygon is allowed to increase without bound, the polygon approaches circular properties. We say the circle is the limiting bevahiour of this process. This exercise has become known as the Process (or Method) of Exhaustion. Stated loosely algebraically, if we let `P_n` be an `n`-sided regular polygon, and `C` be the circle,
Antiphon's Process of Exhaustion. Calculus' central concept is the notion of a limit. This project conveys the idea of a limit through geometric animation. Antiphon (5th Century BC) is credited with the demonstrating that if the number of sides of a regular polygon is allowed to increase without bound, the polygon approaches circular properties. We say the circle is the limiting bevahiour of this process. This exercise has become known as the Process (or Method) of Exhaustion. Stated loosely algebraically, if we let `P_n` be an `n`-sided regular polygon, and `C` be the circle,
`C=lim_{n\to \infty}P_n`
Task.
- Embed within your Catalog Project a new Activity class entitled, ProcessOfExhaustion.
- R. Solway's (RSGC '15) animation (right) starts with a blue circle and both an inscribed (red) and circumscribed (blue) square, centered on the circle.
- As the animation evovles, the number of sides of the two squares doubles with every frame to a reasonable number, say 64.
- Your frames are to be saved as PoE_00.gif, PoE_01.gif and so on, and assembled into an animated gif with a reasonable frame delay.
- You have one month from the date of commitment to submit exemplary, working Catalog source code and, if you can, the animated gif, ProcessOfExhaustion.gif.

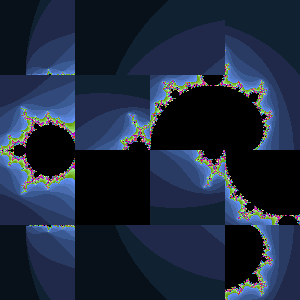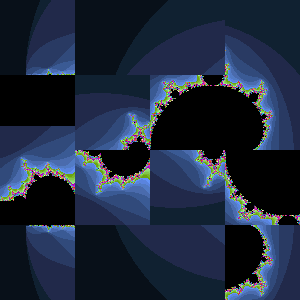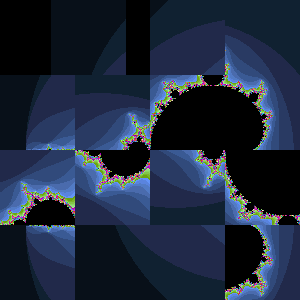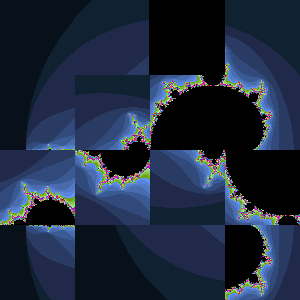
 Mandelbrot. In this project you are asked to port your JavaScript code for the Mandelbrot Set over to Java.
Mandelbrot. In this project you are asked to port your JavaScript code for the Mandelbrot Set over to Java.
Task.
- Create the project, Mandelbrot, and drop in a driver structured along the lines of Graphics.java developed in class this past week.
- Name the frame appropriately.
- Add an instance of a JPanel class to your frame that results in either a black&white rendering of the Set or an esthetically-pleasing coloured one if you are sufficiently inspired.
- Before exiting your JPanel's paintComponent method, add a call to a saveImage method that results in a saved image of the Set under the filename, Mandelbrot.gif.
- Document fully and submit the best code you can.
 Elective. (Status: CLOSED) The first ACE to commit to this Project in an email to me can use a successful implementation of this task to improve his mark on either a previous or future assignment. (Programmer: TG. Start: September 26. Finish: October 26)
Elective. (Status: CLOSED) The first ACE to commit to this Project in an email to me can use a successful implementation of this task to improve his mark on either a previous or future assignment. (Programmer: TG. Start: September 26. Finish: October 26)
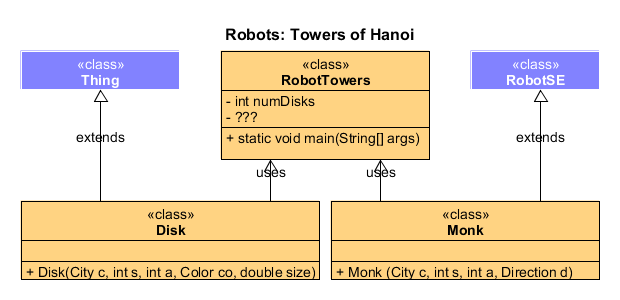
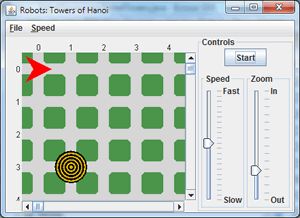
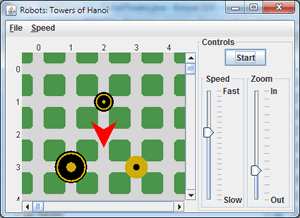
Robots: Towers of Hanoi. For those longing for the simpler days of such Robot classics as SaveThePlanet and CampusCleanUp comes the retro project: RobotTowers.
Task.
- Create a Becker-aware project called RobotTowers and drop in this undocumented driver.
- As you can see (above, left) the City object has 8 circular disks on Peg A at (3,1) of decreasing size. The disks alternate in Color between black and ACES gold (0xCEAA08).
- The Monk object is required to move the disks from Peg A to Peg B at (1,2) using Peg C at (3,3) as the temporary peg, according to the conventions of the 'game'.
- The monk's behaviour is to be directed recursively.
You have one month from the date of commitment to submit exemplary, working source code.
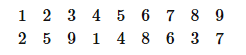
 Parity of a Permutation. Shuffling a given set of elements is meant to generate a permutation of the set. As we've discovered this week, a permutation of a set can be classified as having either even or odd parity, with both occuring in equal number across the collection of all `n!` possible permutations of a set of `n` distinct elements.
Parity of a Permutation. Shuffling a given set of elements is meant to generate a permutation of the set. As we've discovered this week, a permutation of a set can be classified as having either even or odd parity, with both occuring in equal number across the collection of all `n!` possible permutations of a set of `n` distinct elements.
The purpose of this assignment is to demonstrate a single random shuffle of a set of elements and identify its parity as either even or odd. Before you begin, you may want to confirm manually that the parity of the permutation arising from a shuffle of the first 9 natural numbers above right is odd.
Task.
- Familiarize yourself with the both the original Fisher-Yates shuffle and the modern algorithm that improves the order of complexity from `O(n^2)` to `O(n)`.
- Create the Java project, Parity, that implements a single shuffle (permutation) of an array of the first 9 natural numbers using the modern algorithm for the Fisher-Yates shuffle.
- Your code will determine the parity of the resulting shuffle. You may recall the concept of random vs deterministic algorithms was introduced.
- Your project should display, to the Console Window, the initial order of the elements of the array, the order after the shuffle, and the identification of the parity of the latter as either even or odd.
- Incorporate elements of good coding principles and document fully. I expect to receive seven good submissions, with as many as possible one could classify as great.
- Finally, consider the question that was posed in class on Thursday, "Does every interchange of a pair of elements in a set change the parity of the permutation?" In the body of your email provide an answer to this question and your explanation.
 Three Recursive Classics. Given what lies ahead for students
with your academic ability, it is appropriate to confront some
of the classic
recursive problems in our field at this time. Whereas countless internet sites
offer ready-to-go solutions to these gems, conquering these problems on your
own
rewards you with
a sense of scholastic satisfaction unlike few others. More importantly, undertaking
deep analysis of simple problems builds the essential problem-solving Catalog
you'll need to tackle more advanced challenges that lay ahead for which
solutions may not be readily
available.
Three Recursive Classics. Given what lies ahead for students
with your academic ability, it is appropriate to confront some
of the classic
recursive problems in our field at this time. Whereas countless internet sites
offer ready-to-go solutions to these gems, conquering these problems on your
own
rewards you with
a sense of scholastic satisfaction unlike few others. More importantly, undertaking
deep analysis of simple problems builds the essential problem-solving Catalog
you'll need to tackle more advanced challenges that lay ahead for which
solutions may not be readily
available.
We have determined from previous efforts that a successful recursive solution
to a problem defined as a function of n, lies in the discovery of
a two-part, piecewise solution consisting of
the base case (typically, but not limited to, n=1)
and the inductive case (a simpler problem expressed in
terms of n-1). For each of the problems below, challenge yourself to find
this piecewise solution
with pencil and paper. Once
you do,
your coded
solution
will likely yield the correct result on the first run. Create a project entitled, RecursiveClassics, and drop in this driver.
 1.
The Euclidean Algorithm (pp. 90-92). At
the very least, all natural numbers share a common factor of 1. Euclid discovered
the
property
that the
greatest common divisor of two integers a and b,
1.
The Euclidean Algorithm (pp. 90-92). At
the very least, all natural numbers share a common factor of 1. Euclid discovered
the
property
that the
greatest common divisor of two integers a and b, gcd(a,b),
not both of which are zero, is the largest positive integer that divides both a and b.
The Euclidean algorithm for finding this greatest common denominator
of a and b is as follows:
Divide a and b to obtain the integer quotient q and
the remainder r, so that a=qb+r (if r=0, gcd(a,b)=b).
Then gcd(a,b)=gcd(b,r). Replace a and b with b and r and
repeat this procedure.
Because the remainders are decreasing, eventually a remainder of 0 will result.
The last nonzero remainder is gcd(a,b). For example,
1260 = 198⋅6+72 GCD(1260,198) = GCD(198,72)
198 = 72⋅2+54 = GCD(72,54)
72 = 54⋅1+18 = GCD(54,18)
54 = 18⋅3+0 = 18
(
Note: If either
a or
b is negative, replace them with their
absolute values in this algorithm.)
Develop
the driver class RecursiveClassics that will solicit any two
natural numbers (use JOptionPane's
showInputDialog method). A
call to your gcd(a,b) method
will return the greatest common divisor of the two parameters. Finally,
suggest the likely
Big-O
of the Euclidean algorithm method
before researching the answer. PLace the answer in javadoc comment of the method.
 2. Towers of Hanoi (pp. 564-565). Legend has it that a Brahman monk
was charged with the task of moving 64 golden disks (of increasing
diameter from top to bottom) from one post to another
post. The two stipulations placed on the task were that only one disk
could be moved at a time, and no disk of greater diameter could rest on top
of one
with
of
lesser
diameter.
A third post is always available for temporary placement. Task.
You are display the moves necessary to complete the task. Code
the recursive method below into your
2. Towers of Hanoi (pp. 564-565). Legend has it that a Brahman monk
was charged with the task of moving 64 golden disks (of increasing
diameter from top to bottom) from one post to another
post. The two stipulations placed on the task were that only one disk
could be moved at a time, and no disk of greater diameter could rest on top
of one
with
of
lesser
diameter.
A third post is always available for temporary placement. Task.
You are display the moves necessary to complete the task. Code
the recursive method below into your NumericalMethods class,
/*********************************************************************
* This method displays the specific moves necessary to move n rings *
* from the source post to the destination post using a temporary *
* post. The big-O of this task is O(?) *
* @param n the number of disks *
* @param src the name of the source post *
* @param dst the name of the destination post *
* @param tmp the name of the temporary post *
*********************************************************************/
public static void showMoves(int n, char src, char dst, char tmp)
Add statements to your RecursiveClassics driver that will solicit
the number of disks to be moved and a subsequent call the showMoves method as
follows,
showMoves(n,'A','B','C');
For n=3, your output should read,
Move A to B
Move A to C
Move B to C
Move A to B
Move C to A
Move C to B
Move A to B
 3. Permutations (p. 557). Last week we reviewed how the leaves
of a binary decision tree could contain each of the permutations of
a set consisting of 3 unique elements. We confirmed that
a set of 3 unique elements yielded 3! or 6 leaves. In this exercise you will
display all permutations of the characters of a given String.
3. Permutations (p. 557). Last week we reviewed how the leaves
of a binary decision tree could contain each of the permutations of
a set consisting of 3 unique elements. We confirmed that
a set of 3 unique elements yielded 3! or 6 leaves. In this exercise you will
display all permutations of the characters of a given String.
Task. Read the author's description of his algorithm and study his code. Once confirmed, add this code to your RecursiveClassics driver (adding the static keyword to method headers) as well as the comment below, or one in your own words.
/*********************************************************************
* This method displays all permutations of the StringBuffer str *
* The big-O of this task is O(?) *
* @param str the String whose permutations are to be displayed *
* @param n the length of the substring of str under consideration *
*********************************************************************/
public static void permutations(StringBuffer str, int n)
For the string "ABC", the output should read,
BCA
CBA
CAB
ACB
BAC
ABC
Insight into a recursive design. For the string "ABC" there
are 3! or 6 permutations. These appear as leaves in the tree below.
At each stage of n, a loop is engaged that swaps the last character in the string
will all others,
calling the method each time with a reduced n, and swapping them back upon its
return.

 4. Base Conversion. The adajcent algorithm demonstrates a technique for converting a non-negative decimal (Base 10) integer to its binary (Base 2) equivalent.
4. Base Conversion. The adajcent algorithm demonstrates a technique for converting a non-negative decimal (Base 10) integer to its binary (Base 2) equivalent.
Task.
Implement the technique as a recursive method that accepts a number and the target base. Return to the RecursiveClassics project from earlier in the year and incorporate the style of the sample code below to demonstrate conversion from decimal to ternary (Base 3).
public static void main(String args[]) {
int number = 6;
int base = 2;
System.out.printf("%d(10) = %s(%d).\n", number, convert(number,base), base);
}
/**
* Implements a recursive approach to base conversion
*
* @param num the number to convert
* @param base the target base
* @return the converted number
*/
private static String convert(int num,int base) {
...
}
 Perfect Powers. This is a fairly straightforward coding task once you've organized your thinking. To add additional value to the effort, refresh your strong HTML skills by placing your responses to questions 2 and 5 in the opening javadoc of the class.
Perfect Powers. This is a fairly straightforward coding task once you've organized your thinking. To add additional value to the effort, refresh your strong HTML skills by placing your responses to questions 2 and 5 in the opening javadoc of the class.
 Develop an inductive expression for perfect cubes, `C_n`, in a manner similar to our in-class development of the formulas for the perfect triangles, `T_n` and the perfect squares, `S_n`.
Develop an inductive expression for perfect cubes, `C_n`, in a manner similar to our in-class development of the formulas for the perfect triangles, `T_n` and the perfect squares, `S_n`.- Looking at the three inductive formulas you have in front of you (`T_n`, `S_n`, and `C_n`) explain the role played by Pascal's Triangle.
- Write your inductive expression for the perfect cubes, `C_n` from Step 1 as a piecewise recursive mathematical function (PRMF) suitable for coding.
- Use this observation to write PRMFs for perfect fourths and fifths.
- What does the algebra of the perfect fourths formula suggest about the geometry of the fourth dimension?
- Create the project, PerfectPowers, drop in this driver, and complete the bodies of the required methods. Document fully and think deeply for the best results.
 Review. Create the project,
Review. Create the project, Review. Using the references cited, review and (where requested) implement documented code for each of the following. Have your solutions ready for presentation and discussion on September 8-10.

- Primitive Data Types (Reference). Review the complete contents of Reference page.
- Explain why the ranges of (signed/unsigned) )integer values makes sense.
- Which of the four integer data types would be required hold an RGB color value?
- Define the colour constant for the RGB value halfway between black and white
- Characters. (Reference: ASCII, Unicode)
- Review the ASCII Table
- Which Unicode code pages correspond most closely with the Basic and Extended ASCII Character sets?
- Console output. (Reference). Review the contents of this page.
- In a single best-practices statement, display the Pythagorean Theorem and give an example.
- In a single best-practices statement, display the interior degree measures of an isosceles right triangle.
- Operators. (Reference). Familiarize yourself with as much of content of this table as you can.
- Identify the four major categories of operators
- Design an efficient expression that swaps the high and low bytes of the (
short) variable, data.
- Think of two ways to determine whether an integer value is odd.
- Think of two ways to divide an integer variable by 8.
- Decisions. (Reference)
- Assume you have three int variables, a, b, and c. Develop and decision tree (nested if-else statements) that, when executed, results in a having the largest value, b, the middle value and c, the smallest value.
- Iteration. (Reference)
- Display the factors of a variable of type int.
- Determine the number of set bits (1s) in a variable of type, long.
- What is the order, O(n) of your previous algorithm? Can it be improved?
- Methods. (Reference)
- Design and implement the method setBits(long number) that returns the result requested in the second bullet of the previous topic.
- Design and implement the method nextChar(char ch) that returns the next printable character in the Basic ASCII table (efficiently account for the wraparound from 127>32)
- Recursion. (
 Reference)
Reference)
- Develop the recursive method, goldenRatio(int n) that returns an appoximation to φ defined by the continued fraction, GR-2, found here.
- Classes. (Reference)
- Develop the class, Component, that could be used as a basis for defining objects that abstact common components that populate a Grade 10's Evil Genius breadboard.
- Refamiliarize yourself with the resources in Java's static Math and Color classes.
- Objects. (Reference)
- Provide interesting instantiations of various objects of your Component class defined in the previous section.
- Data Structures: Arrays (Reference)
- Define an integer array literal and code an iteration to display its elements
- Define a double matrix literal and code a nested iteration to display its elements two different ways (for and enhanced for)
- Complete these exercises

 Create a class
Create a class 



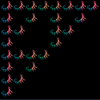

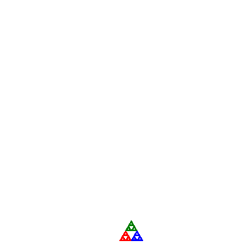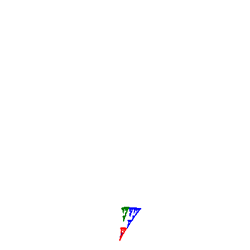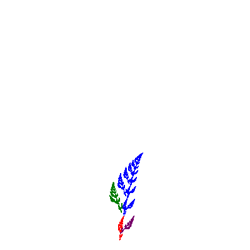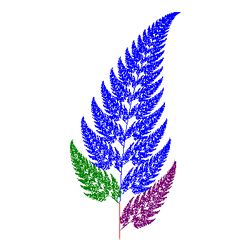





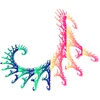















 Add a new menu to the immediate right of Koch,
entitled Lindenmayer.
Add a new menu to the immediate right of Koch,
entitled Lindenmayer.












 Complete this Cantor Set investigation with pencil & paper. (
Complete this Cantor Set investigation with pencil & paper. (






 Combination Lock II. Visualization of Combination Entry. The goal of Part II of the Combination Lock project is to present an accurate rotation of the dial of your Dudley lock as required for any user-requested combination.
Combination Lock II. Visualization of Combination Entry. The goal of Part II of the Combination Lock project is to present an accurate rotation of the dial of your Dudley lock as required for any user-requested combination.


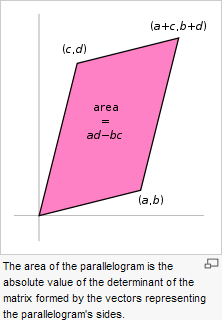
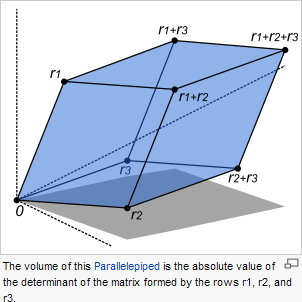
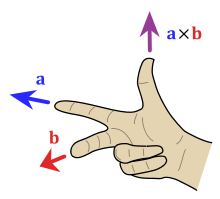 Remember
the crossing pattern in the
Remember
the crossing pattern in the 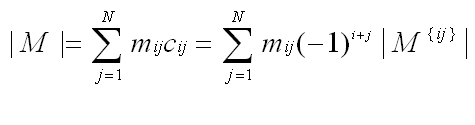


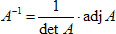
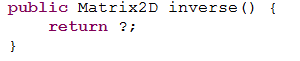
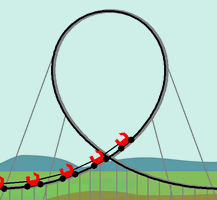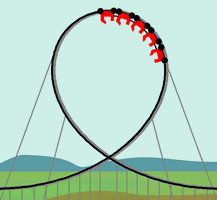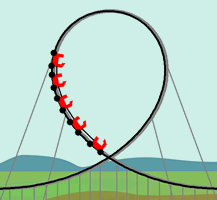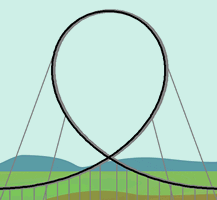















 Add a
Add a 

 Being the highest level class in the application, the
Being the highest level class in the application, the  Antiphon's Process of Exhaustion. Calculus' central concept is the notion of a limit. This project conveys the idea of a limit through geometric animation. Antiphon (5th Century BC) is credited with the demonstrating that if the number of sides of a regular polygon is allowed to increase without bound, the polygon approaches circular properties. We say the circle is the limiting bevahiour of this process. This exercise has become known as the
Antiphon's Process of Exhaustion. Calculus' central concept is the notion of a limit. This project conveys the idea of a limit through geometric animation. Antiphon (5th Century BC) is credited with the demonstrating that if the number of sides of a regular polygon is allowed to increase without bound, the polygon approaches circular properties. We say the circle is the limiting bevahiour of this process. This exercise has become known as the 

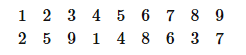
 1.
The Euclidean Algorithm (pp. 90-92). At
the very least, all natural numbers share a common factor of 1. Euclid discovered
the
property
that the
greatest common divisor of two integers a and b,
1.
The Euclidean Algorithm (pp. 90-92). At
the very least, all natural numbers share a common factor of 1. Euclid discovered
the
property
that the
greatest common divisor of two integers a and b, 

