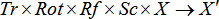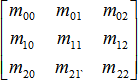DETERMINISTIC IFS ALGORITHM

1. Yale: Affine Transforms preserve collinearity and parallelism. These include scalings, reflections, rotations, and translations. Review the Geometry of Plane Transformations.
2. Yale: The Deterministic Algorithm

   

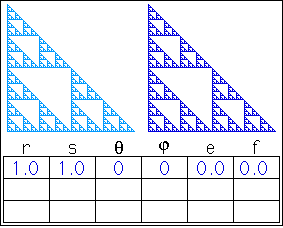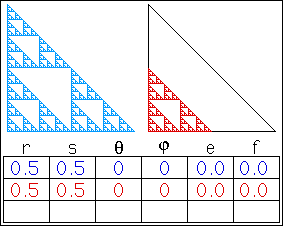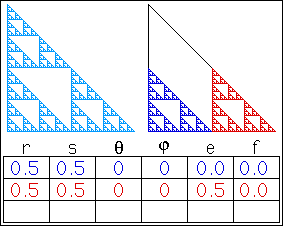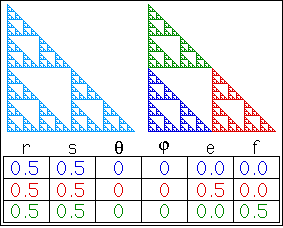
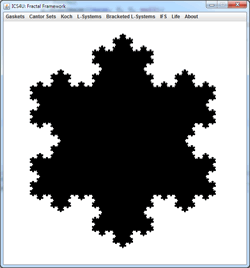
3. Yale. Using their Deterministic IFS Applet, select Selections | Sierpinski Gasket and study the generation animation. From Edit | Affine Transforms and confirm the details. Study the other items from the Selection Menu. Click on the image below to view a Deterministic transition from the Koch Snowflake to a Sierpinski Gasket.

   

4. IFS Freestyle. Read over the section entitled How Do You use IFS Freestyle? Generate the Sierpinski Gasket above using the IFS Freestyle applet. Press Show IFS Code to, again, confirm the details of the 3 affine transformations.

RANDOM IFS ALGORITHM

5. Yale..."Whereas the Deterministic IFS Algorithm renders a picture by,
   1. applying all the rules to any initial picture
   2. then applying all the rules to the resulting picture,
   3. and continuing this process."
   the Random IFS Algorithm takes a different approach to arrive at a (similar) attractor.
6. Yale. Open up their Random IFS Applet and play. Under the Edit| Affine Transforms, modify the Point Size for an interesting effect.
7. If you're feeling ambitious, use Scenarios | Blank to enter one from the internet (a number of examples can be found halfway down Paul Bourke's site). If you need more space, just click OK, and bring up the Edit | Affine Transforms menu again - it will give you 4 more blank transform lines.
8. IFS Freestyle. Test your understanding of the influence of The Collage Theorem on IFS by composing you own using the IFS Freestyle applet to create an original image.
9. The Collage Theorem. With two approaches for applying a given set of affine transformation to produce a target image, we can consider the inverse problem - discovering the set of transformations from a target image. The Collage Theorem provides such a solution requiring the following steps.
   1. Through visualization, identify self-similarities within the image. i.e. parts that are affine contractions of the whole.
   2. Create contracted polygonal copies that tiling the orignial image as snugly as possible with minimal overlap.
   3. Determine the six affine transform value for each contraction.
   4. In the case of the Random IFS algorithm, define a set of probabilities that roughly reflects their relative areas, sum that the sum of the probablities is exactly 1.
10. Study the image below for self similar subimages that involve scaling, rotation, reflection and/or translation of the whole and then use IFS Freestyle to see how close you can came.

    

CATALOG INTEGRATION

1. From Step 1 of Session 1, the domain of the affine transform can be considered as follows.

   

2. Considering we adopt a transformational order similar to Yale's in which we employ scalings first, reflections second, rotations third, and translations last, as in,

   

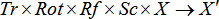
   we end up with a common representation of the matrix equations as expressed as follows.

   

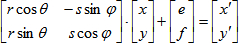
   However, our Matrix2D class encapsulates a 3×3 matrix into which all transformations can fit! Correlate the expressions from above with the elements of our Matrix2D object below.

   

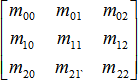
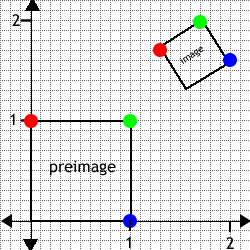
3. Transform2D. Since your Matrix2D class can solve systems of equations, it would be instructional to use your tools to determine an affine transformation for a specific situation. Add statements to your Transform2D driver to determine the 6 crucial elements of the affine transformation matrix that will map the preimage to the image in the graphic below.

   

4. Yale. Their Affine Transform Calculator can also be used to determine the domain of the affine transformation matrix. (Note: I have an email into Dr. Frame at Yale pointing out a small error in the affine transform of Set 1. You are invited to find the error yourself and email me the correction)
5. Here's a good one for February 14.
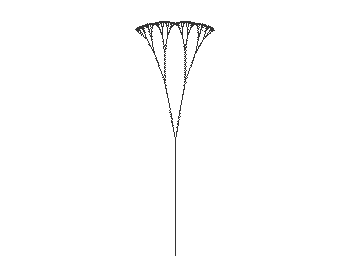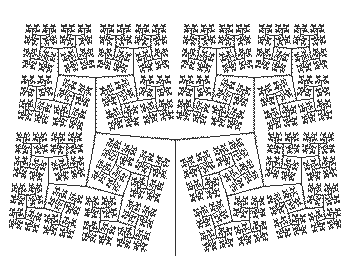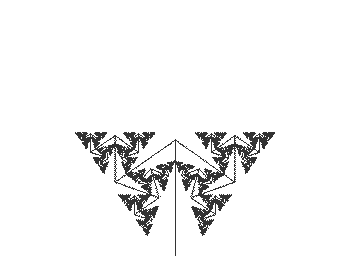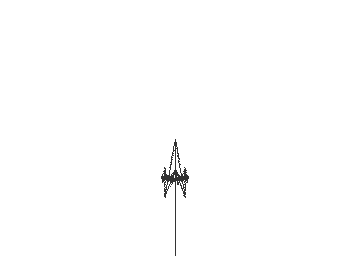