| 2013-2014 ICS4U SOFTWARE ENGINEERING TASKS |
TASK 'CHALLENGE' RATING (offered
to assist you with project management strategies) |
||
Routine |
Typically some deep thinking required,
but not necessarily a lot of coding. |
|
Hard |
Likely involves either a multiplicity
of (possibly new) concepts or algorithms. Allow time. |
|
Buckle Up |
Start immediately, think
deeply, employ a stepwise refinement strategy and post concerns
as required. |
|
![]() Jumble. I've often wondered, "What word in the English language has the most permutations that are also words?". You are asked to develop code to inform you and I, both. You'll make maximum use of the data structures and algorithms we've examined this year. To keep things reasonable, you'll restrict yourself to four-letter words.
Jumble. I've often wondered, "What word in the English language has the most permutations that are also words?". You are asked to develop code to inform you and I, both. You'll make maximum use of the data structures and algorithms we've examined this year. To keep things reasonable, you'll restrict yourself to four-letter words.
Task.
You are free to design and implement the project as you see fit, as long as you use a java.util.TreeSet<E> for one aspect. Your documentation will include clear and full justifications for the structures and code decisions you made.
Finally, you may or may not need this but I found myself thinking about how to construct a balanced Binary Search Tree from an ordered list. A balanced tree optimizes the search time. I googled it and found some interesting suggestions here:
Create a Balanced Binary Tree from a Sorted Linked List
![]() Manual Creation and Traversal. In this first assignment, you are to
incorporate TreeNode.java, exactly
as it appears on page 583 (get student files from Skylight),
into the development of a BST class
whose source code prototype appears below. The BST constructor
will use one statement to construct a tree with
four nodes. Complete the body of the traverse(TreeNode
node) method and use the driver
file, BSTTest.java to
test that the characters appear on the console in alphabetic order.
Manual Creation and Traversal. In this first assignment, you are to
incorporate TreeNode.java, exactly
as it appears on page 583 (get student files from Skylight),
into the development of a BST class
whose source code prototype appears below. The BST constructor
will use one statement to construct a tree with
four nodes. Complete the body of the traverse(TreeNode
node) method and use the driver
file, BSTTest.java to
test that the characters appear on the console in alphabetic order.
public class BST {
private TreeNode root;
/**
* Constructs a BST object encapsulating a binary search tree
* into 'root'. Hard codes the Character data: 'J', 'A', 'V', 'A'
* as the node values in one statement (manually).
*/
public BST() {
}
public void traverse() {
traverse(root);
}
private void traverse(TreeNode node) {
// add recursive code here so that all names are displayed to the console
}
}
![]() AP Exam Prep. This year's AP Computer Science Exam will be written in the morning of Tuesday May 6th. This gives us 3 weeks of preparation.
AP Exam Prep. This year's AP Computer Science Exam will be written in the morning of Tuesday May 6th. This gives us 3 weeks of preparation.
 CodeBug. April 25. In this project you are asked to develop and manipulate an instance of the CodeBug class, defined as,
CodeBug. April 25. In this project you are asked to develop and manipulate an instance of the CodeBug class, defined as,

The CodeBug constructor will receive a String-encoded path it is expected to follow encoded as a String. For example, the CodeBug in the image to the right is just about to complete a figure 8 as a result of this instance's constructor receiving the String: 0123432107654567, where 0 means NORTH, 1 means NORTHEAST, 2 means EAST and so on. Each digit is to interpreted as a direction to face, followed by a move. Digits in the String can be repeated for extended moves in the same direction. You can assume that there is only one CodeBug is the world and it is conveniently positioned in the ActorWorld so it won't hit a boundary in completing its pattern.
Develop documented implementations of the CodeBug class and a driver class CodeBugRunner. Your driver should include a couple of original patterns, with all but one commented out. The patterns should provide a closed loop meaning your CodeBug will return to it's starting point before repeating the pattern indefinitely. Submit the source code for the classes to handin before the start of Wednesday's class and we'll sample a few.
 Gridworld UML: Not assigned. While consulting the Gridworld Javadoc, use the UML Drawing Applet to construct a FULL UML diagram for the Gridworld Case Study that includes all classes and interfaces. Colour the background of all classes and interfaces that are tested on the A exam in orange; those that are not tested in blue. You do not need to include the constructors and methods, this is simply an important exercise to gain an understanding of the organization of the classes and interfaces. Have your .uxf file with you at the start of our Friday class.
Gridworld UML: Not assigned. While consulting the Gridworld Javadoc, use the UML Drawing Applet to construct a FULL UML diagram for the Gridworld Case Study that includes all classes and interfaces. Colour the background of all classes and interfaces that are tested on the A exam in orange; those that are not tested in blue. You do not need to include the constructors and methods, this is simply an important exercise to gain an understanding of the organization of the classes and interfaces. Have your .uxf file with you at the start of our Friday class.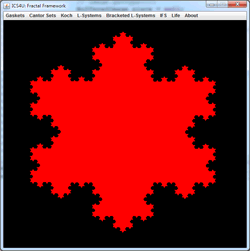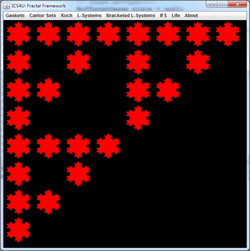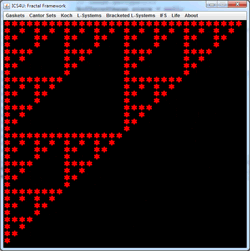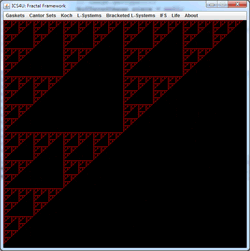
![]() Deterministic IFS: Iterated Function Systems.
Each iteration of the Random IFS algorithm requires the selection and application of only one affine transformation within the code, based on an array of probabilities.
Deterministic IFS: Iterated Function Systems.
Each iteration of the Random IFS algorithm requires the selection and application of only one affine transformation within the code, based on an array of probabilities.
If each iteration of the IFS algorithm requires the application of ALL of affine transformation within the code, randomness is set aside and the outcome is predetermined. For this reason, this strategy is referred to as the Deterministic IFS algorithm.
At each stage of the animation to the right, the entire panel is subjected to three affine transformations resulting in contraction mappings that yield the familiar Sierpinski gasket. What becomes clear is that regardless of the initial image, the final image (the attractor) remains predetermined. View the 2014 ACES IFSDeterministic Gallery below to verify this property.
Task.
public BufferedImage getIFSImage()to your IFSRandom class that will render an image to an off-screen BufferedImage object and return it. You'll use this image as the starting point for each of your preferred Deterministic IFS renderings.
AffineTransform[] transforms; AffineTransformOp[] ops;
| CA | PH | WK | RM | ZR | SR | CS |
|---|---|---|---|---|---|---|
 |
Coming Soon |
 |
 |
 |
 |
 |
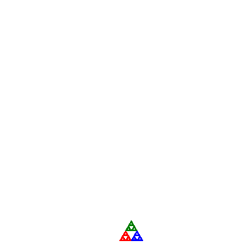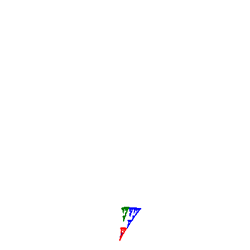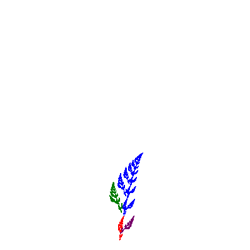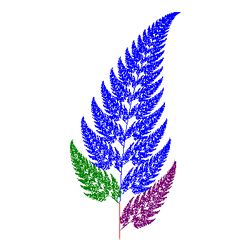
![]() Random IFS: Iterated Function Systems.
With the conceptual and mathematical foundations
laid, you can now undertake the final phase of this year's Fractal Framework
application to render (somewhat realistic) natural forms.
Random IFS: Iterated Function Systems.
With the conceptual and mathematical foundations
laid, you can now undertake the final phase of this year's Fractal Framework
application to render (somewhat realistic) natural forms.
Task.
public class IFS extends Plane2D implements Drawable {
with a constructor possibly of the form,
public IFS(String n, Code code, int iterations, double distance,
double xOffset, double yOffset)
public IFSRandom(String n, Code code, int iterations, double distance,
double xOffset, double yOffset)
library.put("SierpinskiIFS", new Code(new double[][] {
// r,
{ 0.5, 0.0, 0.0, 0.5, 0.0, 0.0 },
{ 0.5, 0.0, 0.0, 0.5, 0.5, 0.0 },
{ 0.5, 0.0, 0.0, 0.5, 0.0, 0.5 } }, new double[] { 0.3333,
0.3333, 0.3334 }));
| CA | PH | WK | RM | ZR | SR | CS |
|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |


![]() LINDENMAYER
SYSTEMS.
With Koch Constructions and the concept of fractal dimension as a foundation,
we can now take one step closer to our goal of rendering of natural forms.
Not surprisingly, credit for this stage goes to a Hungarian biologist/botanist, Aristid
Lindenmayer,
who, in 1968, introduced a formalism associated with the expression of plant
structures, known today as L-Systems. The grammar embodied within
L-Systems lends itself readily to computer graphic rendering.
LINDENMAYER
SYSTEMS.
With Koch Constructions and the concept of fractal dimension as a foundation,
we can now take one step closer to our goal of rendering of natural forms.
Not surprisingly, credit for this stage goes to a Hungarian biologist/botanist, Aristid
Lindenmayer,
who, in 1968, introduced a formalism associated with the expression of plant
structures, known today as L-Systems. The grammar embodied within
L-Systems lends itself readily to computer graphic rendering.
An electronic copy of a wonderful text on the subject of Lindenmayer Systems, entitled The Algorithmic Beauty of Plants (ABOP) is available for download by following the link to the left. The related Algorithmic Botany website offers additional inspiration.
The algorithm for generating these images is defined by an initiator (axiom) and one or more generators (productions) used to propagate the shape over successive generations. In this assignment, we'll use a string for the axiom and a set of production mappings to define the image. A recursive generation algorithm coupled with a character replacement strategy of your choice (see String methods) by their production mappings grows the image. Finally each generation is drawn with a virtual pen (similar to a plotting device) on a JPanel in response to characters in the encoded String. Here is a table containing some of the images you'll be rendering, together with some original curves developed by former ACES. See Framework.html to view the animated renderings.
Figure 1.9 a) |
Figure 1.9 b) |
Figure 1.9 c) |
Figure 1.9 d) |
 |
 |
 |
 |
Gettings Original |
Tsuji Original |
Black Original |
Weldon Original |
 |
 |
 |
 |
Ng Original |
Anderson Original |
Houlding Original |
W. Knowles Original |
 |
 |
||
Mahjour Original |
Ringwood Original |
Ruscica Original |
Sansom Original |
 |
 |
Task.
 Add a new menu to the immediate right of Koch,
entitled Lindenmayer.
Add a new menu to the immediate right of Koch,
entitled Lindenmayer.
![]() KOCH
CONSTRUCTIONS: Triadic Koch Snowflake and Quadratic Koch Island.
With a preliminary understanding of the Cantor Set we
are ready to undertake a related set of
fascinating structures attributed to Helmut Koch
that continued to challenge the conventional notion of dimension well
into the 20th Century. Whereas Cantor simply removed the middle third of
a line
segment, Koch proposed that it be replaced
by two segments of equal length.
KOCH
CONSTRUCTIONS: Triadic Koch Snowflake and Quadratic Koch Island.
With a preliminary understanding of the Cantor Set we
are ready to undertake a related set of
fascinating structures attributed to Helmut Koch
that continued to challenge the conventional notion of dimension well
into the 20th Century. Whereas Cantor simply removed the middle third of
a line
segment, Koch proposed that it be replaced
by two segments of equal length.
| Cantor | Koch |
 |
 |
The bridge from Cantor to Koch can be inferred from the graphic below left, that also highlights the recursive application of each strategy. Koch went further. Using each of the three sides of an equilateral triangle (initiator) and recursively applied his replacement strategy (generator) to produce the perimeter of his classic Koch Snowflake (below right).
| Cantor → Koch | Koch Snowflake |
 |
 |
Now it gets really interesting. Koch's replacement proposal opened the door to a variety of generators, one of which led to the Quadratic Koch Island depicted below.
| Island Initiator and Generator | Quadratic Koch Island |
 |
 |
The iconic Triadic Koch Snowflake and Quadratic Koch Island belong to the set of plane-filling curves or PFCs. The realization of this assignment will result in a third menu in your Fractal Framework devoted to a class of PFCs that we'll refer to as Koch Constructions (there's not enough time in this course to investigate 3D space-filling curves (SFCs) but I'd welcome an email from you someday linking me to your future explorations). Rather than simply considerthe perimeter, our first investigation of the Snowflake and Island images will focus on the full area of the structures as depicted below.
| Triadic Koch Snowflake | Quadratic Koch Island |
 |
 |
Task.
![]() CANTOR
SETS (Part 3 of 3): Triadic and Quadric Cantor Strategies. Look
at the gif animations below. Execute Framework.jar to see them live. Your
previous experience with the Linear Cantor
Set would
suggest that a recursive removal algorithm could be undertaken to generate
these 2D Cantor Sets as well. Although we don't have the time to pursue an
investigation of the 3D Cantor Set this
year, it may be something you may wish to investigate in the future.
CANTOR
SETS (Part 3 of 3): Triadic and Quadric Cantor Strategies. Look
at the gif animations below. Execute Framework.jar to see them live. Your
previous experience with the Linear Cantor
Set would
suggest that a recursive removal algorithm could be undertaken to generate
these 2D Cantor Sets as well. Although we don't have the time to pursue an
investigation of the 3D Cantor Set this
year, it may be something you may wish to investigate in the future.
| Triadic Cantor (depth=7) | Quadric Cantor (depth=6) |
 |
 |
Task.
 Rename the previous Gaskets menu to Pascal.
Rename the previous Gaskets menu to Pascal.Feel free to execute this version of Framework.jar to see the results for this and the future Cantor fractals.



A checkout line is a FIFO structure, we'll model with a Queue <Customer> object. For the sake of this first version of our BBS we'll assume that only one checkout station is available.
 In
this project, you are to run a one-day simulation of the checkout station,
monitoring and reporting the station's activities, and summarizing the results
at the end of the day. Here's the output from a
sample run.
In
this project, you are to run a one-day simulation of the checkout station,
monitoring and reporting the station's activities, and summarizing the results
at the end of the day. Here's the output from a
sample run.
Task. From the data given to you, customers (instances of the Customer class) arrive in random intervals of 1 to 4 minutes. Also, each customer is serviced in random integer intervals of 1 to 4 minutes. Obviously, the rates need to be balanced for the line length to remain manageable. If the average arrival time is larger than the average service rate, the queue will simply continue to grow. Even with balanced rates, randomness can still cause long lines.
Run a simulation for a 12-hour day (720 minutes). Here's a rough guideline for each minute of the day:

Maintain the necessary data so that at the end of the simulation, the program summarizes results for the following:
Final Recommendations,
Using the driver Simulation.java develop and submit the BigBox.java and Customer.java class files that will yield output similar to the above.

![]() The Josephus Game A bidirectional Ring structure would be a useful container for many applications.
One such classic application is the so-called Josephus Flavius Game. A reasonable introduction to the context can be found at Cut The Knot.
The Josephus Game A bidirectional Ring structure would be a useful container for many applications.
One such classic application is the so-called Josephus Flavius Game. A reasonable introduction to the context can be found at Cut The Knot.
Although our review of the Java Collections Framework in the previous chapter revealed the absence of a such a class, it's not hard to imagine how one could be constructed.
There is no such set of structures known as the JavaScript Collection Framework that I know of but, if there was, and it contained a Ring structure, it might look the one I demonstrate here.
Task.
![]() Combination Lock. Since Java's LinkedList<E> class
maintains this data structure as a doubly-linked list, users can
traverse it forward and backward with the help of a ListIterator<E> object.
Create the project LockTest
and a driver that manipulates
the class, Lock,
defined by the
Combination Lock. Since Java's LinkedList<E> class
maintains this data structure as a doubly-linked list, users can
traverse it forward and backward with the help of a ListIterator<E> object.
Create the project LockTest
and a driver that manipulates
the class, Lock,
defined by the  UML specification below. You will need to complete the conditions
in each of the while statements in the driver for the project to work correctly.
UML specification below. You will need to complete the conditions
in each of the while statements in the driver for the project to work correctly.

With a correct implementation of the Lock class initialized with the combination, 21-32-34, your driver will generate the following output,

![]() Gaskets:
The Chaos Game. Familiarize yourself with this
recreational version of the Chaos Game.
Gaskets:
The Chaos Game. Familiarize yourself with this
recreational version of the Chaos Game.

Tasks.

![]() Gaskets:
Pascal's Carpet.
More secrets remain embedded within Pascal's Triangle.
Look at the Triangle again, focussing on groups of adjacent even numbers.
The resulting image should be surprisingly familiar.
Gaskets:
Pascal's Carpet.
More secrets remain embedded within Pascal's Triangle.
Look at the Triangle again, focussing on groups of adjacent even numbers.
The resulting image should be surprisingly familiar.
Task.

![]() Gaskets:
Pascal's Numbers. You explored Pascal's Triangle earlier in the
course so it won't be too difficult to adapt its generation again as a basis for exploring the first of a number of new Fractal algorithms over the next few months.
Gaskets:
Pascal's Numbers. You explored Pascal's Triangle earlier in the
course so it won't be too difficult to adapt its generation again as a basis for exploring the first of a number of new Fractal algorithms over the next few months.
Task.
 |
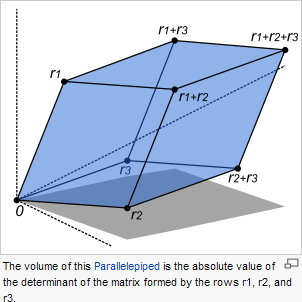 |
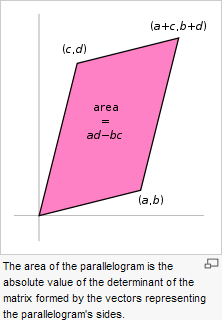
 Remember
the crossing pattern in the Shoelace
Formula for
determining the area of a polygon?
Remember
the crossing pattern in the Shoelace
Formula for
determining the area of a polygon?
 |
![]()
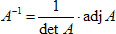
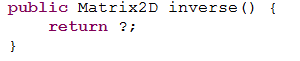

![]() MODELING IN R2: PART 3. Animation2D. In
this final instalment, we integrate the foundation classes
you have developed over the previous two projects to demonstrate the applicability
of matrix-defined transformations to simple, but compelling, two-dimensional
animations.
MODELING IN R2: PART 3. Animation2D. In
this final instalment, we integrate the foundation classes
you have developed over the previous two projects to demonstrate the applicability
of matrix-defined transformations to simple, but compelling, two-dimensional
animations.
Task. Add this driver to your Animation2D Project. Review the driver code. The general idea is to transform one or more Sprite objects to the coordinates for the next frame within the updateScene() method. The loop in the run() method will then call the paintPanel() method in which you can retrieve your Sprite's updated coordinates to populate a Polygon object. This polygon object can be added to the scene through a call to Graphic2D's draw() method.
Here's the full Javadoc. I've created a very elementary example to the right. Considering your vast exposure to gaming animation, I know you'll take your effort to a whole new level.
Note. The classes in this project reflect a strong hierarchical design. I would expect your code to capitalize on the strength of this design; writing clean, tight, efficient carefully-crafted statements that fully exploit the cascading nature of the respective class methods.
Submission. Attach your Animation2D and Sprite classes (and any other previous classes that have been enhanced) to an email to handin with the Subject: Animation2D by the deadline.
Task.
Please attach the separate class files: Transform2D and Point2D, to an email to handin with the Subject: Transform2D by the deadline.
![]() MODELING IN R2: PART 1. Matrix2D. In this 3-part project you are introduced to the matrix algebra of transformational
geometry
leading
to
a creative graphic animation. Below are the submissions of last years' ACES.
Check out more samples from ACES of previous years:
MODELING IN R2: PART 1. Matrix2D. In this 3-part project you are introduced to the matrix algebra of transformational
geometry
leading
to
a creative graphic animation. Below are the submissions of last years' ACES.
Check out more samples from ACES of previous years:
| C. Anderson | P. Houlding | W. Knowles |
 |
 |
 |
R. Mahjour |
Z. Ringwood |
S. Ruscica |
 |
 |
 |
C. Sansom |
||
 |
Task.

![]() Maze Generation and Traversal. We're going to devote the next few classes to a group investigation of mazes: their generation algorithm and solution. This is another classic example of depth-first searching, similar to the recursive flood(x,y) method of last week's PaintBucket activity. In addition to exploring this algorithm, I want to draw your attention to the Processing language. This relatively new Java/C hybrid offers some amazing opportunities and, given your skills, you'll catch on very quickly. The Arduino and Processing languages share the same pedigree, that of the Wiring language.
Maze Generation and Traversal. We're going to devote the next few classes to a group investigation of mazes: their generation algorithm and solution. This is another classic example of depth-first searching, similar to the recursive flood(x,y) method of last week's PaintBucket activity. In addition to exploring this algorithm, I want to draw your attention to the Processing language. This relatively new Java/C hybrid offers some amazing opportunities and, given your skills, you'll catch on very quickly. The Arduino and Processing languages share the same pedigree, that of the Wiring language.
Day 1 (Orientation with Interaction)
 Day 2 (Porting Processing code into your Recursive Framework for maze generation)
Day 2 (Porting Processing code into your Recursive Framework for maze generation)
Day 3 (Developing recursive traversal code for your maze)
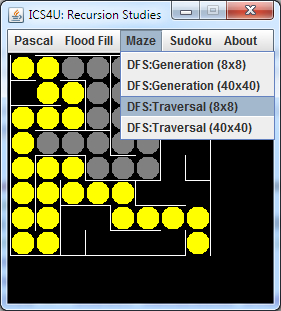 This author provides a very good explanation of the thinking behind recursive strategy to solve the maze (and so many similar problems).
This author provides a very good explanation of the thinking behind recursive strategy to solve the maze (and so many similar problems).

To assist with the evaluation, you will maintain a Stack<Double> to track your progress. The end result of the project will be to animate the collection of intermediate Stack<Double> objects to offer the viewer a play-by-play version of the complete evaluation.
Task.

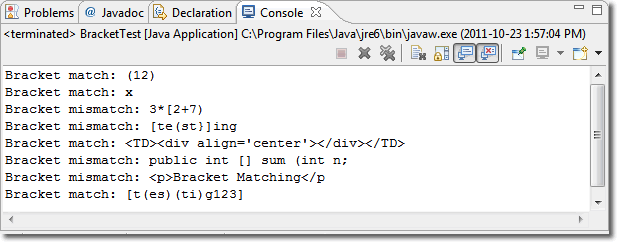
![]() Bracket Matching. The example
method on page 480 offers an iterative solution to confirm whether a String consists of correctly matched parentheses. It would be more impressive if
it were recursive.
Bracket Matching. The example
method on page 480 offers an iterative solution to confirm whether a String consists of correctly matched parentheses. It would be more impressive if
it were recursive.
Task.
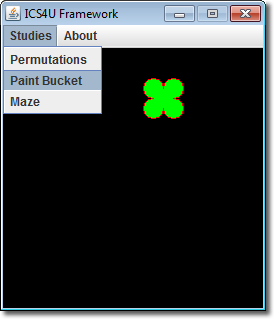
In this assignment you are to flood a region by implementing a depth-first recursive search for a border colour, painting pixels as you go. This is not how it's done in general but, for small areas, it serves as a useful introduction to depth-first recursive searching. For your regions, you can use one of the standard Graphics2D Shape classes ( ie, Rectangle2D, Ellipse2D, Arc2D, etc.) to create an interesting outline of your own design using piecewise Shape objects. Keep your outline small since the system stack has to store many return addresses to manage the depth of recursion.
Task.
Finally, don't forget to update your home page prior to submitting your source code.
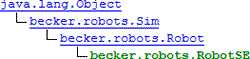
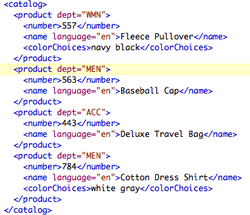
![]() Directory Listing. Nested or 'hierarchical' structures are all around us. Also referred to as tree structures, these organizational arrangements are inherently recursive. Three examples appear below. In each of these, the level of indentation reflects the parent-child relationship.
Directory Listing. Nested or 'hierarchical' structures are all around us. Also referred to as tree structures, these organizational arrangements are inherently recursive. Three examples appear below. In each of these, the level of indentation reflects the parent-child relationship.
| Eclipse: Package Explorer | Becker: RobotSE | XML Catalog |
|---|---|---|
 |
 |
 |
Task.
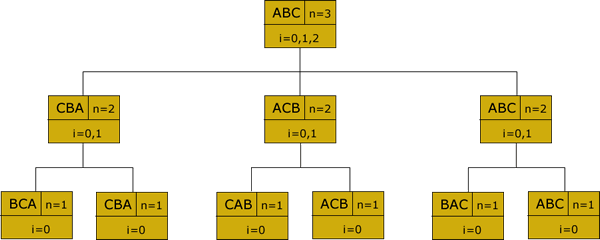
![]() Permutations. A binary decision tree designed to order three unique elements yields 3! or 6 leaves. The leaves can be interpreted as all possible permutations of the original elements and can easily be extended to n unique elements. In this exercise you will
display all permutations of the characters of a given input string.
Permutations. A binary decision tree designed to order three unique elements yields 3! or 6 leaves. The leaves can be interpreted as all possible permutations of the original elements and can easily be extended to n unique elements. In this exercise you will
display all permutations of the characters of a given input string.
Task. As the first entry into your Framework project, display all permutations of a string submitted by a user. For the string "ABC" the output should read,
BCA CBA CAB ACB BAC ABCInsight into a recursive design. For the string "ABC" there are 3! or 6 permutations. These appear as leaves in the tree below. At each recursive level with decreasing n, a loop is engaged that swaps the last character in the string with all others and swapping them back upon its return.
Tasks.

![]() Towers of Hanoi. Legend has it that a Brahman monk
was charged with the task of moving 64 golden disks (of increasing
diameter from top to bottom) from one post to another
post. The two stipulations placed on the task were that only one disk
could be moved at a time, and no disk of greater diameter could rest on top
of one
with
of
lesser
diameter.
A third post is always available for temporary placement. Task.
You are display the moves necessary to complete the task. Code
the recursive method below into your
Towers of Hanoi. Legend has it that a Brahman monk
was charged with the task of moving 64 golden disks (of increasing
diameter from top to bottom) from one post to another
post. The two stipulations placed on the task were that only one disk
could be moved at a time, and no disk of greater diameter could rest on top
of one
with
of
lesser
diameter.
A third post is always available for temporary placement. Task.
You are display the moves necessary to complete the task. Code
the recursive method below into your NumericalMethods class,
/********************************************************************* * This method displays the specific moves necessary to move n rings * * from the source post to the destination post using a temporary * * post. The big-O of this task is O(?) * * @param n the number of disks * * @param src the name of the source post * * @param dst the name of the destination post * * @param tmp the name of the temporary post * *********************************************************************/ public static void showMoves(int n, char src, char dst, char tmp)
Add statements to your RecursiveClassics driver that will solicit
the number of disks to be moved and a subsequent call the showMoves method as
follows,
showMoves(n,'A','B','C');
For n=3, your output should read,
Move A to B Move A to C Move B to C Move A to B Move C to A Move C to B Move A to B
![]() Binomial Theorem. A deep understanding
of
the
Binomial
Theorem
will
prove
useful to you in the months and years ahead. You'll undertake a computational
investigation
of the Binomial Theorem
in this two-part project. Note: For
our
purposes,
we'll
favour recursive strategies
over
iterative implementations strictly for the experience. Here's a reasonably
compact
definition of the Binomial Theorem,
Binomial Theorem. A deep understanding
of
the
Binomial
Theorem
will
prove
useful to you in the months and years ahead. You'll undertake a computational
investigation
of the Binomial Theorem
in this two-part project. Note: For
our
purposes,
we'll
favour recursive strategies
over
iterative implementations strictly for the experience. Here's a reasonably
compact
definition of the Binomial Theorem,
 |
(BT-1) |
Application of (1) yields familiar binomial expansions,
 |
(BT-2) |
Part 1. Combinatorics. Consider the following definition from the field of Combinatorics,
 |
(BT-3) |
The left side of (3) is read as n choose r and represents the number of combinations of n one can make, choosing r items at a time (the last two expressions are different ways of expressing the same concept). As can be seen, the determination of this integer result relies on factorials. For example, assuming 5 students show up for class and I need to choose 2 students to go down to Bloor and pickup the sushi order I placed for lunch. How many ways can the pair of students be chosen? There are 10 such combinations as can be seen below.
 |
(BT-4) |
BinomialTheorem that exercises the
methods in your static NumericalMethods class below. Create
a static NumericalMethods class
and add the following methods, /*************************************************************************** * This method determines the value of n!, recursively * * Precondition: n>=0 * * Postcondition: the method returns the value of n! * * @param n the whole number for which the factorial is to be determined * **************************************************************************** public static int factorial(int n) /**************************************************************************** * This method returns the number of combinations that can be expected given * * n items, taken r at a time. This does not need to be recursive. * * Precondition: n>=0, 0<=r<=n * * Postcondition: the method returns the value of nCr * * @param n the number of items from which combinations are taken, n>=0 * * @param r the number of items taken, 0<=r<=n * ***************************************************************************** public static int choose(int n, int r)
 Now
you will display Pascal's Triangle. Add the non-recursive method below to your
Now
you will display Pascal's Triangle. Add the non-recursive method below to your BinomialTheorem driver,
/********************************************************************** * This method displays a number of rows of Pascal's Triangle *
* Precondition: rows>0 * * Postcondition: the method displays the requested number of rows of * * Pascal's Triangle. It relies on the choose method * * @param rows the number of rows to be displayed * *********************************************************************** public static void pascalsTriangle(int rows)
Finally, indicate the Big-O of each of the three methods above in their respective javadoc comment.
Part 2. Probabilities. In Part 1, each element in Pascal's Triangle was determined through the use of the non-recursive definition in BT-3.
NumericalMethods class.
Add the Big-O of this method
to the javadoc comment.
/********************************************************************** * This method recursively determines the element of Pascal's Triangle * * in the nth row, rth column. * * Precondition: n>=0, 0<=r<=n * * Postcondition: the method return the element of Pascal's Triangle * * in the nth row, rth column * * @param n the row number * * @param r the column number * *********************************************************************** public static int pascal(int n, int r)
/*************************************************************************** * This method returns the String representation of the r'th term of the * * Binomial Theorem of (a+b)^n * * Precondition: a, b the String equivalents of the binomial's terms * * n>=0, 0<=r<=n * * Postcondition:the method returns the String representation of the r'th * * term of the expansion of (a+b)^n. * * @param a the first term in the binomial (a+b) * * @param b the second term in the binomial (a+b) * * @param n the degree of the binomial expansion * * @param r the required term in the binomial expansion, 0<=r<=n * **************************************************************************** public String binomialTerm (String a, String b, int n, int r) /*************************************************************************** * This method returns the full binomial expansion of (a+b)^n as a String * * Precondition: a, b the String equivalents of the binomial's terms, n>=0 * * Postcondition:the method returns the String representation of the * * expansion of (a+b)^n * * @param a the first term in the binomial (a+b) * * @param b the second term in the binomial (a+b) * * @param n the degree of the binomial expansion * **************************************************************************** public String binomialExpansion (String a, String b, int n)
![]() The Golden Ratio (φ) from a Continued Fraction. A compelling topic in pure mathematics
is Continued
Fractions. The essential idea is that the deeper the
evaluation of these expressions, the better the approximation is to
the ultimate irrational target, or what we prefer to call in Calculus, the limit.
The programmatic evaluation of these expressions is a good fit with your understanding
of recursive methods. Here is one example of the continued fraction leading to the
Golden Ratio.
The Golden Ratio (φ) from a Continued Fraction. A compelling topic in pure mathematics
is Continued
Fractions. The essential idea is that the deeper the
evaluation of these expressions, the better the approximation is to
the ultimate irrational target, or what we prefer to call in Calculus, the limit.
The programmatic evaluation of these expressions is a good fit with your understanding
of recursive methods. Here is one example of the continued fraction leading to the
Golden Ratio.
 |
(GR-2) |
The limit of both (GR-2) and (GR-1) is φ.
Task. To your Recursive Project, implement the class GoldenRatio, the output of which will allow the viewer to confirm that both sequences (GR-1) and (GR-2) converge on φ. Maximize your use of recursive methods. Beyond the correct answer, evaluation of your submission will focus on the elements of good programming: method design, efficient implementation, clearly-labelled output and strong documentation. Finally, keep in mind the following,
![]() The Golden Ratio (φ) from the Fibonacci Rectangle. In class we investigated
the relationship between the sequence defined by the quotients of successive
terms of the Fibonacci sequence
and the Golden Ratio, φ. This can be expressed as the process,
The Golden Ratio (φ) from the Fibonacci Rectangle. In class we investigated
the relationship between the sequence defined by the quotients of successive
terms of the Fibonacci sequence
and the Golden Ratio, φ. This can be expressed as the process,
 |
(GR-1) |
| Fibonacci Rectangle | Square Construction with Compass and Straightedge |
|---|---|
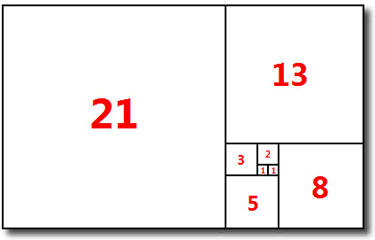 |
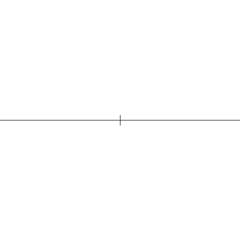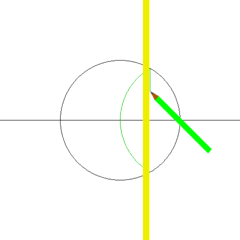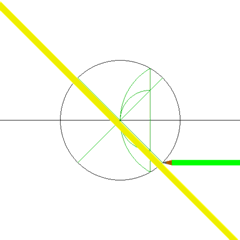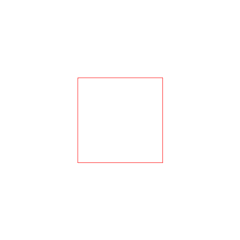 |
Task.
public int fib (int n) that
iteratively determines and returns the nth term of the fibonacci
sequence. What is the Big-O of
this implementation?public
int fib (int n) that
exercises this definition. What is the Big-O
of this
implementation?
![]() Powers. It is virtually impossible to provide practical
programming solutions to a variety of complex problems without recursion.
As such, it is an indispensable programming
strategy.
Having said this, you'll have to decide when it's warranted.
Successful implementation of a recursive solution depends on your ability to
define a recursive solution on paper.
For example, the power function, xn can be defined iteratively (non-recursively) as,
Powers. It is virtually impossible to provide practical
programming solutions to a variety of complex problems without recursion.
As such, it is an indispensable programming
strategy.
Having said this, you'll have to decide when it's warranted.
Successful implementation of a recursive solution depends on your ability to
define a recursive solution on paper.
For example, the power function, xn can be defined iteratively (non-recursively) as,
Defined recursively, we could write,
| (P-1) |
From (1), the implementation is straightforward. Successful recursive solutions arise from the programmer being able to express a definition similar to (1) for each new problem, that includes both the general recursive substitution expression and a basis or stopping condition.
Tasks.
public int powerIterative(int x, int n) that
determines and returns the value of xn, iteratively. What is the Big-O of this implementation?public int powerRecursive(int x,
int n) that determines and returns the value of xn, recursively. What is the Big-O of this implementation?public int pow2(int n) that computes the value of 2n with
a running time of O(1).