TASK 'CHALLENGE' RATING (offered to assist you with project management strategies)
	Routine	Typically some deep thinking required, but not necessarily a lot of coding.
	Hard	Likely involves either a multiplicity of new concepts and/or new mathematical concepts or algorithms.
	Really Hard	Start immediately, think hard, employ a stepwise refinement strategy and post concerns as required.
		The best way to describe these assignments is...

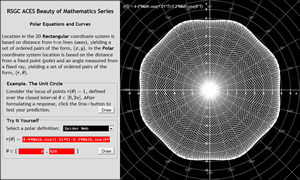
Polar Equations. Location in the 2D Rectangular coordinate system is based on distance from two lines (axes), yielding a set of ordered pairs of the form, `(x,y)`. In the Polar coordinate system location is based on the distance from a fixed point (pole) and an angle measured from a fixed ray, yielding a set of ordered pairs of the form, `(r,theta)`.

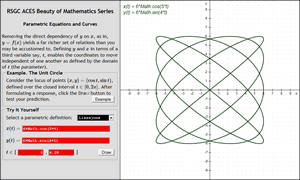
Parametric Equations. Removing the direct dependency of `y` on `x`, as in, `y=f(x)` yields a far richer set of relations than you may be accustomed to. Defining `y` and `x` in terms of a third variable say, `t`, enables the coordinates to move independent of one another as defined by the domain of `t` (the parameter). Loci defined this way take on the definition, `(x,y)=(f(t),g(t))` or simply, `(x(t), y(t))`.

The parametric curve that appears to the right and below is a member of a family of parametric equations known as a Lissajous (or Bowditch) figure. Our adapted technique for capturing Canvas frames to an animated gif to present a dynamic display of the drawing in the image to the bottom right.

New JavaScript Concepts

• Associative Arrays
• Dynamic population of select form control
• eval()
• String: replaceAll

Controller Task.

1. The basis for this project can be carried forward from Canvas Preview in which we developed the page, QuadraticFunctionwithCanvas.html. Here's a link to Stevie's.
2. Copy the BoM page ParametricEquations.html. Be sure your page is MathJax-enabled. Here's the original reference page we used a few months back...
3. Create a Description Panel similar to the one above right.
4. Review the concept and syntax of a JavaScript Associative Array, define catalog as one, and populate it with a few literal objects as follows,

    

   // define a catalog of parametric equations as an associative array using literal objects
   var catalog = new Array();
   catalog['Unit Circle'] = {x:'Math.cos(T)', y:'Math.sin(T)', tMin:0, tMax:6.28, dt:0.1, width:2, stroke:'#000'};
   catalog['Ellipse'] = {x:'8*Math.cos(T)', y:'6*Math.sin(T)', tMin:0, tMax:6.28, dt:0.1, width:2, stroke:'#606'};
   catalog['SuperEllipse'] = {x:'Math.pow(Math.abs(Math.cos(T)),0.5)*8*Math.sign(Math.cos(T))', y:'Math.pow(Math.abs(Math.sin(T)),0.5)*6*Math.sign(Math.sin(T))', tMin:0, tMax:6.28, dt:0.1, width:2, stroke:'#606'};
   

5. Add a populateSelect() function that will obtain a reference to your select control, prior to implement a for (var name in catalog) iteration that will stock your select control with the name indices of your array of parametric definitions.
6. Initialize the text fields in your Description Panel to the essential parameters of the first entry in your catalog. Implement an onchange() event handler that with repopulate the text inputs with the essential details of the user-selected parametric equation.

Model Task.

1. Back in December, we undertook the group effort, Quadratic Function: Vertex Form, the code for which you have mounted on your website. If you recall, we used this project to dig deeply into JavaScript objects, as can be seen from the code fragment below,

   // define a catalog of parametric equations as an associative array using literal objects
   grid = new Grid('dot',0.5,'black');
   axes = new Axes('cartesian',xMin,xMax,yMin,yMax,1,1,'black',font);
   locus = new Locus('cartesian',quadratic, xMin, xMax, 'red','italic normal 12pt Arial');
   plot = new Plot(canvas,'#FFF','cartesian',grid,axes,quadratic,null);
   plot.draw();
   

   This group of objects collaborated to render a quadratic object literal, the definition of which looked something like the following,

   quadratic = {
   	a:1,
   	b:6,
   	c:9,
   	disc:function(){
   		return this.b*this.b-4*this.a*this.c;
   	},
   	natureOfRoots:function(){
   		d = this.disc();
   		if(this.a==0)
   			return "One root; this is not a quadratic function"
   		if (d<0)
   		  return "No real roots";
   		else if (d==0)
   		return 'Two equal real roots';
   	return 'Two distinct real roots';
   	},
   	f : function(x){
   		return this.a*x*x+this.b*x+(1*this.c);
   	},
   	defn : function(){
   		ret = "f(x) = ";
   		ret += (this.a == 1 ? "" : this.a == -1 ? "-" : this.a <=0 ? this.a :this.a);
   		ret += "x^2";
   		ret += (this.b == 1 ? "+x" : this.b == -1 ? "-x" : (this.b==0 ? "" : this.b>1 ? ("+"+this.b+"x") :"-"+Math.abs(this.b)+"x"));
   		ret += (this.c== 0 ? "": this.c>0 ? "+"+this.c : this.c);
   		return ret;
   		},	
       root1 : function(){
   		denominator = 2*this.a;
   		if (d<0){
   			return (-this.b/denominator)+"-"+(Math.sqrt(-this.disc())/denominator).toFixed(3)+"i";
   		}
   		return (-this.b-Math.sqrt(this.disc()))/denominator;
   	},
   	root2 : function(){
   		denominator = 2*this.a;
   		if (d<0){
   			return (-this.b/denominator)+"+"+(Math.sqrt(-this.disc())/denominator).toFixed(3)+"i";
   		}
   		return (-this.b+Math.sqrt(d))/denominator;
   	},
   
   
   	toString: function(){
   		summary = "Summary...\n";
   		summary += "\nNature of Roots: "+this.natureOfRoots();
   		//added a protection against it being a straight line
   		if(this.a!=0){
   			summary += "\nRoot 1: "+this.root1();
   			summary += "\nRoot 2: "+this.root2();
   			summary+= this.yInt();
   			summary+= this.parabolaOpen();
   			if(this.natureOfRoots()!="No real roots"&&this.a!=0){
   				summary+= "\nAxis of symmetry: x = "+this.axisOfSymmetry();
   				summary += "\n"+this.vertex();
   			}
   		}
   		return summary;
   	},	
   		//returns the axis of symmetry for the parabola
   	axisOfSymmetry:function(){
   			return (this.root1()+this.root2())/2;
   
   	},
   
   	//returns the y-intercept as a coordinate
   	yInt:function(){
   		var cUse= (+this.c);
   
   		return "\ny-intercept: (0.000, "+cUse.toFixed(3)+")";
   	},
   
   	//returns which direction the parabola opens from
   	parabolaOpen:function(){
   		if(this.a>0)
   			return "\nParabola opens: upward";
   		else if(this.a<0)
   			return "\nParabola opens: downward";
   		else
   			return "";
   	},
   	vertex:function(){
   		var xvalue = this.axisOfSymmetry();
   		return "Vertex: ("+xvalue+", "+this.f(xvalue)+")";
   	}
   };// quadratic
   

2. Copy your Grid, Axes, and Locus object definitions from your QuadraticFunctions page and paste them, without modification, into your ParametricEquations page.
3. The equivalent to the quadratic object literal for this project is, naturally, parametric, the structure of which appears below (the body of the xt and yt functions should be apparent). Add this definition to your ParametricEquations.html page and ensure the browser loads the page without error.

   parametric = {
   	x:'',
   	y:'',
   	tMin:0,
   	tMax:0,
   	dt:1,
   	width:1,
   	stroke:'#F00',
   	font: 'italic normal 12pt Arial',
   	xt : function(t){
   		// TBD
   	},
   	yt : function(t){
   		//TBD
   	},
   	xdefn : function(){
   		return "x(t) = "+this.x;
   	},
   	ydefn : function(){
   		return "y(t) = "+this.y;
   	}
   };
   
     

4. The body of Plot's draw() function looks like the code below. For the start of Monday's class, please have your ParametricEquations.html working to the point that the background, grid and axes are displayed and there are no other errors.

       this.draw = function(){
        this.drawBackground();
        this.drawGrid();
        this.drawAxes();
        //this.drawLocus();
       }; // draw
   

View Task.

It's time to put it all together. With the body of the xt and yt function complete, uncomment the this.drawLocus() statement of plot's draw() function to produce a rendering of the parametric curve on your canvas.

Reexamine the design of plot's drawLocus() function from your previous QuadraticFunction project. As can be seen, the gist is to prepare for the start of the graphing through a call to your context object's beginPath() function and the subsequent setting of the value of the parameter t to the start of the domain interval, prior to obtaining the initial x and y values.

These (and every other (x,y) pair) are mapped to screen coordinates before calling the moveTo method. For the balance of the drawing, a loop undertakes a walkthrough of the domain interval, increasing t by dt with each iteration, prior to calculating, mapping and drawing a line to, the next ordered pair.

When the upper end of the domain interval is reached, the loop terminates, the strokeStyle and lineWidth settings are applied and the path drawn (stroke). Finally, the definition of the locus should be presented at the top left corner.

Submission.

1. Your catalog of parametric curves should offer at least 10 entries. Scour the internet for interesting curves. Originality matters.
2. Be sure your page offers users the ability to edit the parametric definitions of `x(t)` and `y(t)` as well as the bounds of the domain of `t`.
3. You may also wish to offer the user the ability to enter a value for `dt`.
4. You are not required to integrate the drawing with an animation, nor are your expected to integrate a gif capture of the rendering. On the other hand for those students with time on their hands and have unnatural affinity for perfect marks, these would be compelling enhancements.

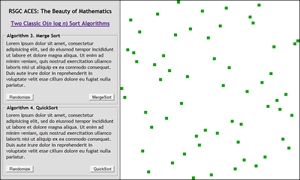
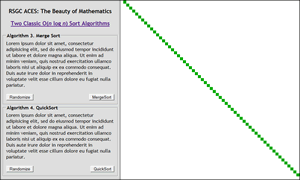
Sort Algorithms 2. O(n log n): Merge Sort. In this second look at sorting algorithms you will investigate the use of recursion to improve the Big O from O(n²) to O(n log n). You are required to undertake your implementation and visualization (below, left) of the Merge Sort. The Quick Sort (the fastest alrogthm yet devised) is left to you to implement for your own edification.

Merge Sort	QuickSort

Task.

1. Create the page SortingAlgorithms2.html that appears similar to the images below, replacing the Latin dummy text with your description of the Merge Sort algorithm. (for the QuickSort description simply suggest a future implementation). Hyperlink the subheading to http://en.wikipedia.org/wiki/Sorting_algorithm.

2. Implement an MVC strategy similar to the one you employed in Sort Algorithms 1 this past weekend that will result in a visualization of the Merge Sort algorithm for the user-selected number of elements.
3. One change you'll make for this implementation will be the data you record for later animated playback. For your Selection and Insertion Sort Algorithms, you first created a working copy of the randomized array, sorted it, and recorded the indices of each swap. The Merge Sort Algorithm does not lend itself easily to this tactic. Instead, it will be easier to record a duplicate of the entire state of the array after each merge is completed, hence no working copy needs to be created. The resulting array of arrays will be sufficient, making this animation function more straightforward.

Sort Algorithms 1. O(n²): Selection Sort and Insertion Sort. Consider populating an array with the first 150 whole numbers. If the array was shuffled prior to representing each number on a 600 x 600 canvas as 4 x 4 rectangle in which the column is 4 times (Thanks, Robbie) the index of the number within the array and the row is 4 times the number, you would achieve the image to the bottom left. If you then applied a sort algorithm to the array and displayed it again, in the same fashion, you would achieve the image in the bottom right (the factors 150 and 4 of 600 should be controlled by the user).

Task.

1. I created the image to the right as a view of the Insertion Sort as it might appear on a 3x3 matrix of 8x8 LED Matrix blocks developed by one of our hardware ACES! Anybody????
2. Create the page SortingAlgorithms1.html that appears similar to the images above. Hyperlink the subheading to http://en.wikipedia.org/wiki/Sorting_algorithm
3. Replace the Latin dummy text with your description of each algorithm.
4. Implement the two sorting algorithms as discussed in class that results in an animated depiction of the strategy (use RequestAnimationFrame()), in the manner I have done.
5. After popluating an appropriately-sized array (the model), you will first execute each sort algorithm, independent of their canvas presentation. While doing so, you will record the two locations of each swap in a separate array. It is this sequence of exchanges that your animation callback function later draws on next, to present the visualization (the view). This strategy prerecord/playback strategy underpins many of the future algorithms we'll explore - this year and next - so you need to condition yourselves to it. So, to recap, first instantiate an array to hold the swaps (as literal objects), as in,

   swaps = new Array();

   Next, you don't sort the original array, you first obtain a working duplicate of the array and sort it, to obtain the sequence of swaps. When your algorithm determines it's appropriate to exchange the contents of locations a and b, you do so, and register the swap as follows, either,

   swaps[index++] = {loc1:a,loc2:b};

   or, as Greg wisely suggested,

   swaps.push({loc1:a,loc2:b});

   When the algorithm is finished, you can then apply the array of swaps to the original array to support your animated view/visualization.
6. Finally, since both the Selection and Insertion sort algorithms involve the generation of a swap sequence, you are to use the same animate callback function for both strategies.

Binary Search Algorithm. Add the Binary Search feature to your SearchAlgorithms.html page. Again, offer your viewers an animated display of the Binary Search algorithm using an array of objects as your container. Use the recently introduced window.requestAnimationFrame() technique.

You are NOT expected to implement a recursive binary search strategy as we discussed in Exercise 2. Binary Search of this week's Recursive Binary Exercises case study. However, if you were to do so, you could invoke a recursive binary search function, storing the sequence of indices encountered in an array as we did in Step 6. This prerecording could then be used as a reference for playback from within your animate function.

You are not restricted to using bottom-aligned rectangles, but you are to retain the fill colors that I have employed for consistency of viewing (red as the current object, green as the target and blue for the remaining elements). Be creative.

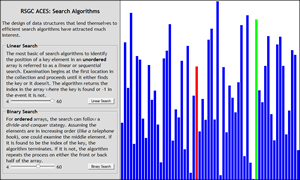
Linear Search Algorithm. (Try to write great code) Create the BoM page: SearchAlgorithms.html. Apart from keeping the topology of the BoM page intact (Description panel on the left, 600x600 Canvas panel on the right), you are free to demonstrate your coding and creative skills in this project. On a single page, you are asked to offer users an animated display of the Linear (Sequential) Search alogrithm using an array of objects as your container. Use the newly introduced window.requestAnimationFrame() technique. You are not restricted to using bottom-aligned rectangles, but you are to retain the fill colors that I have employed for consistency of viewing (red as the current object, green as the target and blue for the remaining elements). Be creative. Links you may wish to consider include,

1. RSGC ACES: ICS3U Framework (under Searching, naturally)
2. Your textbook: Chapter 2. Drawing (You'll find many familiar images and techniques used in ViaCAD)
3. Drawing Shapes with Canvas
4. Math.random(). Does Javascript offer a random seed method?
5. (Our next area of investigation) Sorting Applets
6. (Advanced) Boyer-Moore String Search Algorithm

Pascal's Carpet. In completing Exercise 3. Pascal's Carpet of the previous in-class assignment, you will draw a closer connection between the Triangles of Sierpinski and Pascal. Task. Click on the image to the right to view the final state of the Canvas after either the Animated or Instant buttons are selected. The image presents 600 rows of Pascal's Triangle in which only pixels for the odd elements are drawn. Pressing the Instant button will result in the final image appearing all at once. Pressing the Animated button will result in the final image rolling in, row- by-row, on a timed interval Reference.

In Class Assignment: January 31. Light collaboration is permitted for Exercise 1 and 2 ONLY on this page.

Task.

1. Create the BoM page: PascalsTriangleOnCanvas.html.
2. Complete Exercise 1 and 2 below as defined and presented.
3. Chapter 3 in your text (pp. 201-252) offers a comprehenisve treatment of text-handling.
4. This reference offers links in the bottom left corner that cover pretty well everything you'll need to work with fonts on your Canvas.
5. Anthony recommends this tutorial.
6. Use Courier New for your font face.
7. Exercise 3. Pascal's Carpet is left for your own INDIVIDUAL effort, to be submitted on Tuesday February 4. Do NOT mount the page on your web site.

Exercise 1. Left-Aligned	Exercise 2. Center-Aligned

Quadratic Function: Vertex Form. This is an optional assignment for those courageous enough to undertake it. Submission of a successful implementation will not only advance your skill set, but can be used to replace an inferior result from an earlier assignment. Task. Click the adjacent image to enlarge and review the content. This script will enable your users to manipulate the range (slider) controls to affect transformations of the vertex form of the quadratic. The definition in the top left corner will remain presented in standard form. Duplicate the Description Panel simply for the purpose of this submission. If you wish take the project in a different direction afterwards you have my complete support. The deadline for submission to handin is December 21 and you are NOT to mount this project on your web site. Those wishing to undertake this beast are advised to seek clarification of the precise expectations. An in-class demonstration is available upon request.

Sierpinski '2D' Tetrahedron. (Based on the strong design elements put in place over the sequence of scripts leading up to this assignment, you should have little trouble overcoming the 2-diamond rating of this project). The goal is to create the illusion of a 3D Sierpinski tetrahedron from 4-2D Sierpinski triangles. Here is the UML diagram we based our development of the Sierpinski Triangle on and the Sierpinski stamp image. Click on the image to the right to enlarge. Create the page Sierpinski2DTetahedron.html that offers an interesting description of the Sierpinski triangle, our algorithm and a launch button in your Description panel. On launch, your script will invite the user to click on any four canvas points with the mouse. The canvas points will be intepreted as the four vertices of a tetrahedron, giving rise the rendering of the four triangular faces of the structure.

Canvas Preview. Your task is to ensure that the fully-functioning QuadraticFunctionWithCanvas Case Study we undertook together is mounted on your website.

Monday's Test. Your task this week is to read my Feedback email for the test thoroughly and ensure that as many corrections and enhancements as possible have been made and the results are as stable as possible in both Chrome and Firfefox before mounting on your website for my review on Sunday morning. This evaluation is out of 5 and your score will largely reflect the extent to which you have improved your page based on observations contained within my Feedback email.

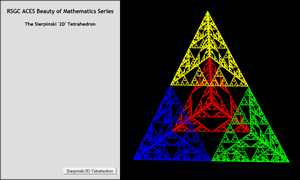BoM: The Quadratic Function. In class this week we examined the use of JavaScript Objects in the context of a first-degree relation (linear). In this assignment you are asked to demonstrate your understanding of Objects (and mathematics) in presenting a page based on a second-degree relation (quadratic).

Task.

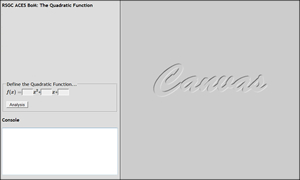1. Create a page entitled, QuadraticFunction.html, similar in topology to the pages we've been using (click on the image to the right to enlarge).
2. After some research, present a concise description, and one or more examples, of a quadratic function, incorporating ASCIIMathML in the process.
3. Duplicate the form.
4. Your script should extract the necessary data from the form's elements and use the information in the creation of a quadratic object that encapsulates the necessary properties and methods to efficiently handle the expectations below.
5. The first line in your Console panel should identify the nature of the roots for which there are three possibilities: two distinct real roots, two equal real roots, or two complex roots.
6. Subsequent entries in the Console panel should provide specific details of the two roots if the discriminant `b^2-4ac>=0`. Remember, a second-degree relation always has two roots (it's simply a matter of the split between real and complex).
7. Submit as required. Do not post your file to your website until Sunday.

BoM: Finite Arithmetic Series. For the first instalment of our Beauty of Mathematics Series you are asked to,

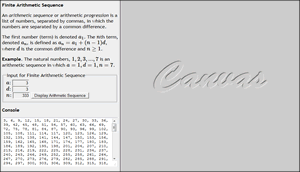1. Develop the page, FiniteArithmeticSeries.html that is similar to the Finite Arithmetic Sequence page completed this week in class (minimal design, ASCIIMathML, forms) that presents the concept of a Finite Arithmetic Series.
2. Challenge yourself to write in, your own words, an opening description of this concept.
3. Familiarize yourself with the syntax of the ASCIIMathML.js library.
4. Submit FiniteArithmeticSeries.html to handin under the Subject Line: Finite Arithmetic Series by the deadline.
5. Please do NOT post your page on your web site until Sunday.

JavaScript: Animation. For this (individual) assignment you are asked to develop a page that offers a creative, interactive animation depicting a scene or activity. Your strategies should have a 3D feel (x,y,z) interval timing of images on layered <div>s. A premium will be placed on creativity, so give the context of your application considerable thought. Like Andrew's recent costume triumph, simple but brilliant.

Create the web page Animation.html. Place supporting files in their respective subfolders: images, css and scripts. Submit all files by the deadline under the required Subject Line.

HTML Forms: Facebook Sign Up. Primarily to gain practice with Forms and to consolidate previous HTML concepts, you are asked to recreate the part of Facebook's home page that appears to the right. Collaborating with your partner to produce IDENTICAL results, complete the task below. Facebook Groups GB TH LD RSa ED RSo ME PW TG AL SB RF AP Create the file, Facebook.html. Duplicate the screen capture to the right using CSS styles matching the fonts, colors, sizes etc. as nearly as your skills will permit. You will need to visit Facebook's home page for the specific details. Each student will attach his group's Facebook.html page (and any supporting files) to an email to handin and mount the page on his website, adding a new link from his home page, by the deadline.

HTML Tables: Circuit Designer. With terrific (free) applications such as Fritzing and 123D Circuits, it's pretty clear that there is a demand for the visual rendering of electronic circuits. In preparation for the day that one of you will write your own interactive web-based assembly utility, we may as well lay a foundation now .A selection of circuit symbols (offered in SVG format) on this Wikipedia page has been coverted to gif for your use.

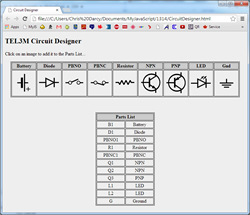Task. The purpose of this page is to allow the user to dynamically assemble a Parts List by clicking on images presented in the symbol table.

1. Create the web page, CircuitDesigner.html and add the elements as seen in the image to the right, up to and including, the header row of the Parts List Table. Feel free to incorporate your own CSS designs (circuitDesigner.css)
2. The Parts List Table starts off with a header row, spanning two columns.
3. Each time the user clicks on an image, a new row is added to the Parts List Table consisting of the code (B, D, R, etc.) in the first column and a single word description (Battery, Diode, Resistor, etc.) in the second column.
4. Variables are to be maintained that keep track of the count of each code and appended to the code prior to display.
5. Submit your file(s) to handin and mount your page on your web site by the deadline.

JavaScript: eReader Simulation. For your first JavaScript assignment you are asked to blend your burgeoning HTML/CSS skills with the concepts you've uncovered within theTry it yourself » examples designed to support the browser's window object properties and methods. Your comprehensive review of these BOM examples will enable you to develop the web page eReader.html that includes the following requirements,

1. Source a large chunk of text (two or more screenfuls)
2. The background colour of the window and the foreground text should be styled in a manner reflective of common eReaders (light gray background, (blackish) enlarged font, increased line spacing, etc).
3. The moment the page loads, the text is smooth scrolling at a rate conducive to easy, stress-free reading.
4. Additional esthetic and creative elements befitting of the talented web designers you are becoming. You may wish to consult references (like this one) for inspiration.
5. Upload your eReader.html page to your Web Publishing folder as close to the Saturday midnight deadline as possible and add a link to it from your home page (similar to updating your ER's TOC!)

Visual Elements: Chapter 4 Case Study.

1. Undertake the Chapter 4 visual enhancements prior to uploading and performing a validation.
2. Make all required corrections.
3. Confirm the link from your home page still functions as expected.

Visual Elements: Presentations. Each of you has been assigned a section within Chapter 4. Please prepare a creative web page, mounted on your website with the URL below, that contains a comprehensive example of the concept you have been assigned. Your code should include on-screen explanations and internal comments in the event viewers wish further detail. Your presentation should last 10 minutes, followed by a five-minute Q&A if necessary.

	#	Section	Details	Presenter	Date
	1	4.1a Horizontal Rule		Eric	Thu Oct 3
Hands-On Practice 4.1
	2	4.1b Borders and Padding		Peter	Thu Oct 3
Hands-On Practice 4.2
	3	4.2a GIF	History, Features, Support	Stevie	Mon Oct 7
	4	4.2b JPG	History, Features, Support	Alec	Mon Oct 7
	5	4.2c PNG	History, Features, Support	Lachlan	Mon Oct 7
	6	4.3a Image Element (Basic)	Attributes, Accessibility	Mariano	Mon Oct 7
Hands-On Practice 4.3
	7	4.3b Image Hyperlink	Optimize for the Web	Roger	Mon Oct 7
Hands-On Practice 4.4
	8	4.4 HTML5 Visual Elements	Figure, Caption, Meter, Progress	Anthony	Wed Oct 9
Hands-On Practice 4.5
	9	4.5 Background Images		Turner	Wed Oct 9
Hands-On Practice 4.6
	10	4.6a Image Maps		Robbie	Wed Oct 9
	11	4.6b Favorites Icon		Robert	Wed Oct 9
	12	4.7 Sources and Guidelines for Graphics			Wed Oct 9
Hands-On Practice 4.7
	13	4.X HTML5: Scalable Vector Graphics		Greg	Fri Oct 11
	14	4.Y HTML5: MathML		Thomas	Fri Oct 11
Hands-On Practice 4.8

CSS: Chapter 3 Case Study.

1. Make sure your Chapter 2 Case Study has been thoroughly validated before beginning with the Chapter 3 upgrades. Make all changes locally.
2. Undertake the Chapter 3 CSS enhancements, prior to uploading and performing the validation.
3. Make all necessary changes and upload one final time.

1. Isolate and save the background image from the Week #3 Lunch Menu to the images folder of laptop version of your Lunch Menu web page.
2. TBC...
3. Upload ??? to your Web Publishing folder and add a link from your home page by the deadline.

1. Chef Corey posted the Week #3 Lunch Menu as an attachment to an email to the News conference on Monday September 16. You are asked to duplicate his Word document as an HTML5 document using ONLY the HTML concepts introduced in Chapter 2.
2. Create a document entitled index.html that will serve as your home page. Create an ordered list of links to your projects this year, adding a link to LunchMenu.html as described in Step 1.
3. Upload both web pages to your Web Publishing folder by the deadline.

HTML: Chapter 2 Case Study. You are asked to complete your assigned Case Study (found on pp. 66-72) by the end of the day, run it through the W3C Validation Service, upload the site to an appropriately-named folder within your Web Publishing folder, and add a link from your index.html home page.

WEB Presentations. We will all participate in bringing the first few weeks of course content to light. The topics below will be assigned to you with the help of our trusty Randomizer. For your assigned task(s), you are asked to ensure the content provided in the text is covered as a starting point, adding a little extra depth and interest resulting from further research into the concepts. You are free to assemble the material in any form you like (ie. Word, web page, PP, email) and sum it up for your peers and I in a 15-minute presentation allotting 10 minutes for content delivery and 5 minutes for Q&A. Note: Be careful not to stray into the content of another student's presentation still ahead of you. In preparing your presentation keep in mind, but do not limit yourself to, content that that your classmates can use to recognize the Key Terms and questions at the end of each Chapter.

	#	Section	Details	Presenter	Date
	1	1.1 The Internet and the Web	Browsers (Popularity)	Anthony	Tue Sep 10
	2	1.2 Web Standards and Accessibility	Universal Design	Stevie	Tue Sep 10
	3	1. 3 Information on the Web	Reliability, Ethics	Eric	Thu Sep 10
	4	1.4 & 1.5 Network Overview	Client/Server Model	Alec	Thu Sep 10
	5	The Cloud		Thomas	Thu Sep 12
	6	1.6 Internet Protocols	HTTP, TCP, IP	Lachlan	Thu Sep 12
	7	1.7 Uniform Resource Identifiers/Locators	Domain Names	Robbie	Thu Sep 12
	8	Commercial Web Service Providers	Registering a Domain Name Services, Costs	Peter	Thu Sep 12
	9	1.8 Markup Languages	HTML, XML, XHTML	Turner	Mon Sep 16
	10	1.9 Web Uses		Greg	Mon Sep 16
	11	The Future of the Web		Mariano	Mon Sep 16
	12	2.1 HTML Overview	HTML>XHTML>HTML5	Robert	Mon Sep 16
	13	2.2 Document Type Definition 2.3 Example XHTML Page 2.4 Example HTML5 Page		Roger	Mon Sep 16