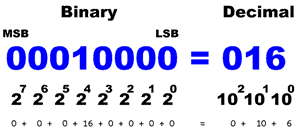 Computer Engineers should be as comfortable with binary, quaternary, octal, and hexademical numbers systems as they are with decimal. For over a decade ACES have undertaken tournaments to promote mastery of base conversion strategies. Initially, Cisco Systems hosted a freely accessible page entitled the Binary Game that they created for their IT Specialists. In 2014, Cisco started requiring users to create a 'free' account to continue accessing this recreational activity. Since ACES are passionate about creating their own hardware and software solutions we created our own class set of handheld, programmable versions of the Binary Challenge. In early 2019, with our 3D printing facilities sufficiently mature, a summer collaboration with one of my talented design students (K. Fiset-Algarvio; ACES '19, Guelph '24) produced cases for a class set 30 RSGC ACES Binary Challenge units, materializing in late August of 2019, just in time for the start of the 2019/2020 academic year. Click on the image to the right to see a detailed photo of our one-of-a-kind training device.
Computer Engineers should be as comfortable with binary, quaternary, octal, and hexademical numbers systems as they are with decimal. For over a decade ACES have undertaken tournaments to promote mastery of base conversion strategies. Initially, Cisco Systems hosted a freely accessible page entitled the Binary Game that they created for their IT Specialists. In 2014, Cisco started requiring users to create a 'free' account to continue accessing this recreational activity. Since ACES are passionate about creating their own hardware and software solutions we created our own class set of handheld, programmable versions of the Binary Challenge. In early 2019, with our 3D printing facilities sufficiently mature, a summer collaboration with one of my talented design students (K. Fiset-Algarvio; ACES '19, Guelph '24) produced cases for a class set 30 RSGC ACES Binary Challenge units, materializing in late August of 2019, just in time for the start of the 2019/2020 academic year. Click on the image to the right to see a detailed photo of our one-of-a-kind training device.
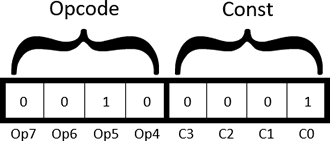
 This device is a prime example of the three domains ACES pursue vigorously: hardware, software, and design. On the software side, these units offer eight distinct 8-bit binary challenges. The external 6-pin ISP header allows for 'in-system' updating of the firmware that you should consider employing for your own future embedded systems projects.
This device is a prime example of the three domains ACES pursue vigorously: hardware, software, and design. On the software side, these units offer eight distinct 8-bit binary challenges. The external 6-pin ISP header allows for 'in-system' updating of the firmware that you should consider employing for your own future embedded systems projects.
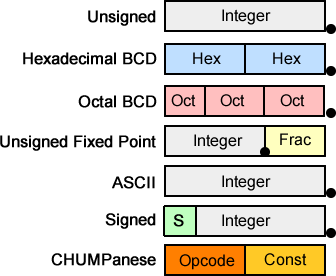
- Unsigned
- Hexadecimal (16) BCD
- Octal (8) BCD
- Quaternary (4) BCD
- Fixed Point (Q5.3)
- ASCII
- Signed
- CHUMPanese
RSGC is extremely fortunate to have this unique training device available, both as a practical instrument for exploring the binary number system from Grades 5-12, but also as a model of the unique secondary school engineering capabilities undertaken in the DES. Perhaps the single drawback is the expense of its creation. At just over $100 for parts alone, coupled with hours worth of 3D printing and manual assembly per unit, these devices are not easily replicated (otherwise, it may qualify as ACES' first Kickstarter initiative due to its unique design and broad appeal).
It is hard to express the degree of pride embodied in this achievement. In the truest sense, our Binary Challenge reflects the enormous advances our ACES program has made over the past 16 years, due largely to the efforts of Georgian ACES and Mr. Paul Elia, our DES Design Consultant.
If you ever find yourself in the area of the DES after school, drop in and try your hand.  Caution: even practicing can be addictive :)
Caution: even practicing can be addictive :)
Functionality
- The I/O power rocker switch is located on the back, closest to the 9V power receptacle. When activated, the green 3mm LED will light.
- The MODE rocker switch, next to the I/O switch, selects between the two games in the current firmware (primary and secondary). When the secondary game is active, the red 3mm LED is lit. Note: toggling between games immediately zeros your SCORE.
- The larger 0.56" blue 4-digit, 7-segment display is the VALUE you are required to emulate using the 8 rocker switches which add the respective binary power weighting to the VALUE.
- The smaller 0.39" green 4-digit, 7-segment display is your SCORE. 30 points are awarded if you achieve the presented VALUE in under 5s, 20 points are awarded if you achieve the VALUE in under 10s, and 10 points are awarded when you achieve the correct VALUE, regardless of how long it takes you.
Seven Binary Challenges
A. Unsigned. This is the plain vanilla, 8-bit positive integer model spanning the closed interval [0,255] in which the binary power weightings are as etched onto the acrylic top and silk screened on the PCB. The binary point is assumed to be to the right of the rightmost switch and all eight switches influence the integer part of the VALUE. Competency: 500 in 5 min.
 B. Hexadecimal (16) BCD. Each VALUE is to be interpreted as a pair of binary coded nibbles presented using the hexadecimal digits, 0..F. Users interpret each set of 4 switches as binary weightings of 8-4-2-1. For example a VALUE of A7 would be represented as 1-0-1-0 0-1-1-1.
B. Hexadecimal (16) BCD. Each VALUE is to be interpreted as a pair of binary coded nibbles presented using the hexadecimal digits, 0..F. Users interpret each set of 4 switches as binary weightings of 8-4-2-1. For example a VALUE of A7 would be represented as 1-0-1-0 0-1-1-1.
Competency: 3000 in 5 min.
C. Octal (8) BCD. Each VALUE is to be interpreted as the Octal (base 8) equivalent of the 8-bit unsigned binary number, presented using the octal digits 0..7. Users interpret the least significant 6 bits as two triples, each with binary weightings of 4-2-1. The most significant 2 bits have a weighting of 2-1. For example, a VALUE of 261 (the octal equivalent of 17710) would be represented as 10 110 001. Competency: 3000 in 5 min.
D. Quaternary (4) BCD. (Added: 2022 09 25) Each VALUE is to be interpreted as the Quaternary (base 4) equivalent of the 8-bit unsigned binary number. Users interpret the eight bits as four pairs of two-bit quaternary digits 0..3. For example, a VALUE of 30214 (the quaternary equivalent of 20110) would be represented as 11 00 10 01. Competency: 3000 in 5 min.
E. Unsigned Fixed Point: Q(5.3). Unless otherwise indicated in a computing context, the binary point is assumed to take up a position to the right of the rightmost bit presented. This is the case with the four challenges described above. However, in some applications, where a limited set of fractional values are still useful, code can implicitly interpret the binary point to be elsewhere! Arithmetic routines can be easily implemented to manipulate the virtual binary point which can provide the foundation for lightning fast calculations. Heer's an ACES primer on the topic. Search for Integer Math in C and enjoy the concept.
To prepare yourself for integer math manipulation, this challenge assumes the binary point is between bit 3 and bit 2 so that only 5 bits (bit 7 to bit 3) contribute to the integer part, leaving 3 bits (bit 2 to bit 0) to provide the fractional part. Under this design we say the range of numbers has a resolution of 1/8 or 0.125. For example, under Q(5.3), the binary representation of 6.875 would be 00110 111 and the representation of 17.375 would be 10001 011.
A further complication for Q(5.3) on our Binary Challenge device is that the VALUE display is only capable of presenting 4 digits (and a decimal point course). So, of the 256 possible configurations of 8 bits, we are limited to those that represent decimal equivalents that require only 4 digits to display. Thus, 6.875 is included but 17.375 is not. This still leaves 168 valid presentatations (more than enough to confirm you understand:). Competency: 2000 in 5 min.
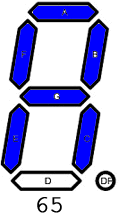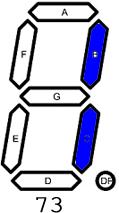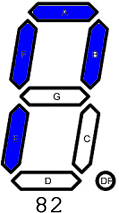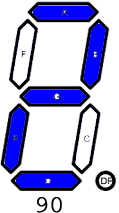
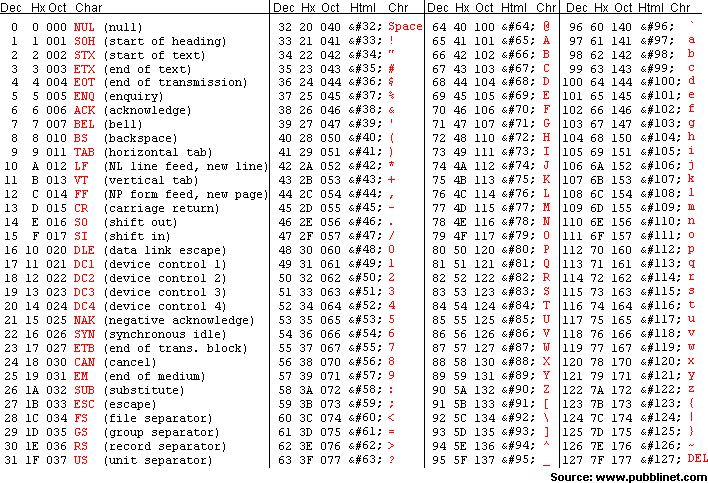
F. ASCII. The VALUE displayed is a 7-segment representation of an uppercase ASCII letter, each of which is depicted in the adjacent animation. Users are required to enter the binary equivalent of the decimal value over the closed interval [65,90] that corresponds to the letter. See ASCII Table at the end. Competency: 2000 in 5 min.
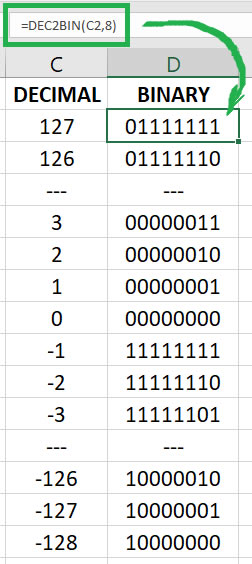
G. Signed. In this challenge, the VALUE display is capable of presenting any of the 256 integer representations of signed 8-bit values under the  2's complement algorithm span the closed interval from [-128,127]. Competency: 1500 in 5 min.
2's complement algorithm span the closed interval from [-128,127]. Competency: 1500 in 5 min.
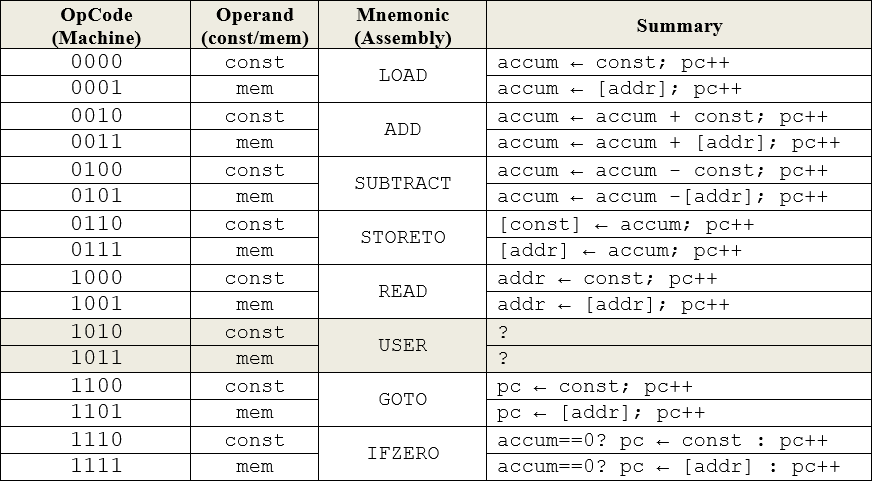
 H. CHUMPanese. Sr. ACES build their own 4-bit programmable computer in their first term. Dubbed the CHUMP by its designer, D Feinberg, the design incorporates an 8-bit RISC Assembly Language that provides, among other advantages, an ideal bridge to AVR Assembly language in the second hafl of their final year. The CHUMP's 16 instructions appear below, left, and a sample program appears below right.
H. CHUMPanese. Sr. ACES build their own 4-bit programmable computer in their first term. Dubbed the CHUMP by its designer, D Feinberg, the design incorporates an 8-bit RISC Assembly Language that provides, among other advantages, an ideal bridge to AVR Assembly language in the second hafl of their final year. The CHUMP's 16 instructions appear below, left, and a sample program appears below right.
To allow Sr. ACES to gain rapid familiarity with both Machine and Assembly language coding of CHUMPanese, a seventh game has been developed to run on our Binary Challenge Devices. The Opcode appears on the VALUE display and the Operand appears on the SCORE display. Users have the standard response time to enter the corresponding machine language instruction, in binary, on the switches. This is not unlike how the first programmers entered their code on computers 70 years ago.
Competency: 1000 in 5 min.
C. D'Arcy. Summer/Fall 2019.
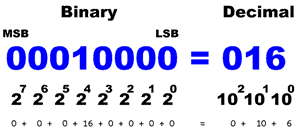 Computer Engineers should be as comfortable with binary, quaternary, octal, and hexademical numbers systems as they are with decimal. For over a decade ACES have undertaken tournaments to promote mastery of base conversion strategies. Initially, Cisco Systems hosted a freely accessible page entitled the Binary Game that they created for their IT Specialists. In 2014, Cisco started requiring users to create a 'free' account to continue accessing this recreational activity. Since ACES are passionate about creating their own hardware and software solutions we created our own class set of handheld, programmable versions of the Binary Challenge. In early 2019, with our 3D printing facilities sufficiently mature, a summer collaboration with one of my talented design students (K. Fiset-Algarvio; ACES '19, Guelph '24) produced cases for a class set 30 RSGC ACES Binary Challenge units, materializing in late August of 2019, just in time for the start of the 2019/2020 academic year. Click on the image to the right to see a detailed photo of our one-of-a-kind training device.
Computer Engineers should be as comfortable with binary, quaternary, octal, and hexademical numbers systems as they are with decimal. For over a decade ACES have undertaken tournaments to promote mastery of base conversion strategies. Initially, Cisco Systems hosted a freely accessible page entitled the Binary Game that they created for their IT Specialists. In 2014, Cisco started requiring users to create a 'free' account to continue accessing this recreational activity. Since ACES are passionate about creating their own hardware and software solutions we created our own class set of handheld, programmable versions of the Binary Challenge. In early 2019, with our 3D printing facilities sufficiently mature, a summer collaboration with one of my talented design students (K. Fiset-Algarvio; ACES '19, Guelph '24) produced cases for a class set 30 RSGC ACES Binary Challenge units, materializing in late August of 2019, just in time for the start of the 2019/2020 academic year. Click on the image to the right to see a detailed photo of our one-of-a-kind training device.