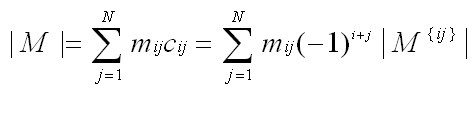ICS4U SOFTWARE ENGINEERING TASKS

TASK 'CHALLENGE' RATING (offered to assist you with project management strategies)
Hard
Typically some deep thinking required, but not necessarily a lot of coding.
Really Hard
Likely involves either a multiplicity of (possibly new) concepts or algorithms. Allow time.
Buckle Up
Start immediately, think hard, employ a stepwise refinement strategy and post concerns as required.

AP Exam Prep. This year's AP Computer Science Exam will be written in the morning of Tuesday May 3rd. This gives us 3 weeks of preparation.

  1. CodeBug. April 11-13. In this project you are asked to develop and manipulate an instance of the CodeBug class, defined as,

    The CodeBug constructor will receive a String-encoded path it is expected to follow encoded as a String. For example, the CodeBug in the image to the right is just about to complete a figure 8 as a result of this instance's constructor receiving the String: 0123432107654567, where 0 means NORTH, 1 means NORTHEAST, 2 means EAST and so on. Each digit is to interpreted as a direction to face, followed by a move. Digits in the String can be repeated for extended moves in the same direction. You can assume that there is only one CodeBug is the world and it is conveniently positioned in the ActorWorld so it won't hit a boundary in completing its pattern.

    Develop documented implementations of the CodeBug class and a driver class CodeBugRunner. Your driver should include a couple of original patterns, with all but one commented out. The patterns should provide a closed loop meaning your CodeBug will return to it's starting point before repeating the pattern indefinitely. Submit the source code for the classes to handin before the start of Wednesday's class and we'll sample a few.

  2. Gridworld UML: April 13-15. While consulting the Gridworld Javadoc, use the UML Drawing Applet to construct a FULL UML diagram for the Gridworld Case Study that includes all classes and interfaces. Colour the background of all classes and interfaces that are tested on the A exam in orange; those that are not tested in blue. You do not need to include the constructors and methods, this is simply an important exercise to gain an understanding of the organization of the classes and interfaces. Have your .uxf file with you at the start of our Friday class.
  3. Sample Exam: April 17. With pencil and paper only, grab the kitchen timer and allow 75 minutes to answer the 40 Multiple Choice questions from Sample Test 1. Take a 15 minute break and then allow yourself 50 minutes to answer the first two Free Repsonse questions from Sample Test 1.
  4. April 23-24. AP A-2. Bring to class on April 27.
  5. April 27-28. 2010 Free-Response Questions. Bring your responses to class on Friday April 29 for discussion and scoring detials
  6. April 30-May 1. 22 FC Questions on page 17. Confirm answers yourself.
Framework: Web Content Update. You are asked to provide as much supporting content and commentary as you can to the various algorithms we studied in our Framework Project. This site will be a valuable asset to to you in the years ahead so please make an effort to put it into top shape. Make the page as navigable as possible with links to external references and internal bookmarks ( ie. <a href = "#top">Top</a>)

The Game of Life. John Conway introduced the world to one of the most studied algorithms within the Cellular Automata family in the October 1970 issue of Scientific American. Read Wikipedia's explanation of the simple rules for propagation. In the applet to the right, I colour-coded the cells as Birth, Survival and Death. Explore the game through either or both of the Explore links on the course page. Give yourself time to enjoy how such an elegantly simple set of rules can produce such fascinating outcomes.

Task.

  1. Add a seventh column to your Fractal Framework applet entitled Life.
  2. Design and implement a Drawable class called Life, modeled after this UML diagram.
  3. Add menu items that include one or more random seeds and a library of a handful of known patterns that you find inspiring. Glider Guns, Puffer Trains, and Tire Tracks are my favorites.

 

The Collage Theorem. TBD.

 

 

 

 

 

 

 

 

 

IFS: Iterated Function Systems. With the conceptual and mathematical foundations laid, you can now undertake the final stage of this year's Fractal Framework application to render somewhat realistic natural forms.

Task.
IFS
Fern #2 (lower)
  1. Add a sixth column to your Fractal Framework applet entitled IFS
  2. Under the IFS menu, add menu items similar to those in the second column of the table to the right.
  3. Add an IFS class that implements the Drawable interface. One design suggestion would be to create a Code class to encapsulate the various affine transformations, their probabilities and the colour palette. All IFS images could be stored in a TreeMap<String,Code> where String is the name of the IFS, thereby making retrieval relatively efficient. This structure could be initialized within the constructor of the Content class.
  4. Provide colorful renderings of the image that make optimum use of the panel.

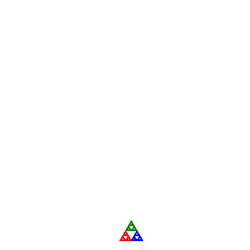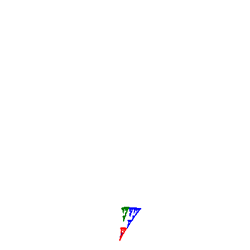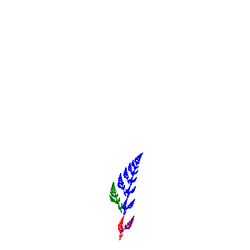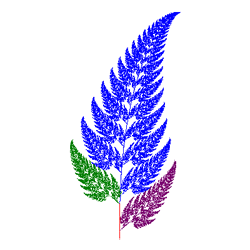
Matrix2D Enhancements. Important enhancements to your Matrix2D class are required to support your investigations of the upcoming Collage Theorem and ultimately, IFS Codes. These include the concept of a determinant and their application in the context of Cramer's Rule and, possibly, the calculation of the inverse of a matrix.

  1. (DAY 1) The Determinant of a Matrix.
    1. Remember the crossing pattern in the Shoelace Formula for determining the area of a polygon?
    2. Another crossing pattern enables the determinaton of the Cross Product of a two vectors. (F = qv × B)
    3. Finally, here's the crossing pattern associated with the evaluation of the determinant of a 3 × 3 matrix.
    4. Unfortunately, this pattern is not scalable and this is the wrong way to find the determinant of a 4 × 4 matrix.
    5. A recursive technique attributed to Laplace (you'll hear much more about his contribution to mathematics next year) is the preferred method for us,

    6. Implement the above definition through the method public double getDeterminant() to be added to your Matrix2D class. Generalize your design so that the determinant of a square matrix of any dimension could be found using the supporting methods highlighted in red in the Explorer view below ( coFactor, determinant, and minor). Add statements at the end of your Matrix2DTest driver to confirm your resuts. Here's a worked example to assist with your development.

  2. (DAY 2) Cramer's Rule.
    1. One method for solving a relatively simple system of n equations with as many unknowns acknowledges Gabriel Cramer (1704-1752) for a computationally-friendly algorithm. Here's a description,
      1. Consider a system represented in the matrix form, Ax=b, where A is the n × n coefficient matrix, x is the variable column vector with n elements and b is the right-side column vector with n elements.
      2. Let Ac be the matrix obtained by replacing column c with b.
      3. Let the determinant of A be represented as D.
      4. Let the determinant of Ac be represented as Dc
      5. Cramer's Rule defines the solution to the system as,


        where D ≠ 0.
    2. Add the method
      3. public double [] cramersRule( double [] b ) to your Matrix2D class that returns the solution x to the system Ax=b , where A is this Matrix2D object. You are to make maximum use of existing Matrix2D resources and keep the rest of your code as tight and efficient as possible. Add a call to Matrix2D's solveSytemmethod (it will simply call cramersRule for now) statements at the end of your Matrix2DTest driver to confirm your resuts.

  3. (DAY 3) The Inverse of a Matrix. Just as a (multiplicative) inverse exists for all real numbers, x, (except 0), so, too, does the inverse of a square matrix A (det A≠0). The inverse of A can be defined as,

    where adj A is the adjoint of A. The adjoint of A is the matrix obtained by transposing the matrix of coFactors of A. Implement the blue DAY 3 methods above, as follows,
    1. the transpose() method reflects the element in the main diagonal. That is, the element at row r, column c is exchanged with the element at row c, column r. NOTE. This would be a perfect opportunity to practice the technique of swapping elements without the use of a third variable.
    2. the scalarMultiple(double k) method simply multiplys each element of the matrix by the scalar parameter.
    3. the adjoint() method simply returns a new Matrix2D object populated with the coFactors of A that have been transposed.
    4. if the previous 3 methods are implemented as recommended, the inverse() method can typed as follows,)

    Add statements to your Matrix2DTest driver to test your inverse() method (make sure to check that the determinant is not 0 beforehand!

BRACKETED LINDENMAYER SYSTEMS. You are now ready to undertake the rendering of primitive plantlike structures similar to the approximation of the tumbleweed to the right.

To facilitate the branching characteristics inherent in plants, L-System productions introduce brackets. Your rendering method will interpret the open bracket '[' as a command to preserve the current drawing state (position, heading, and possibly colour and line thickness), to be restored on the encounter with the next close bracket ']'. In this way, your drawing algorithm can 'return' to a node and continue drawing in another direction. A Stack<Turtle> is a perfect collection for this purpose.

Task.

  1. Under the new menu, Bracketed L-Systems, include menu items corresponding to Figures 1.24a through f as found on page 25 of the Algorithmic Beauty of Plants. Reference: ICS4U Framework Applet.
  2. Without creating a new class, enhance your LSystems draw method to accommodate the additional characters, [ and ] which are designed to preserve and restore the state of the Turtle object
  3. Feel free to experiment with colour, thickness, scale, and position in your rendering of these structures to portray as much realism as you can.
  4. Submit your updated Framework source code to handin and have your web page updated by the deadline.

LINDENMAYER SYSTEMS. With Koch Constructions and the concept of fractal dimension as a foundation, we can now take one step closer to our goal of rendering of natural forms. Not surprisingly, credit for this stage goes to a Hungarian biologist/botanist, Aristid Lindenmayer, who, in 1968, introduced a formalism associated with the expression of plant structures, known today as L-Systems. The grammar embodied within L-Systems lends itself readily to computer graphic rendering.

An electronic copy of a wonderful text on the subject of Lindenmayer Systems, entitled The Algorithmic Beauty of Plants (ABOP) is available for download by following the link to the left. The related Algorithmic Botany website offers additional inspiration.

The algorithm for generating these images is defined by an initiator (axiom) and one or more generators (productions) used to propagate the shape over successive generations. In this assignment, we'll use a string for the axiom and a set of production mappings to define the image. A recursive generation algorithm coupled with a character replacement strategy of your choice (see String methods) by their production mappings grows the image. Finally each generation is drawn with a virtual pen (similar to a plotting device) on a JPanel in response to characters in the encoded String. Here is a table containing some of the images you'll be rendering, together with some original curves developed by former ACES. Run Framework.jar to view the animated renderings.

Figure 1.9 a)
Figure 1.9 b)
Figure 1.9 c)
Figure 1.9 d)
Gettings Original
Tsuji Original
Black Original
Weldon Original
Ng Original

Task.

  1. Add a new menu to the immediate right of Koch Constructions, entitled L-Systems.
  2. Under the L-Systems menu, add menu items for the Koch Snowflake, the Koch Island and each of the images found in Figures 1.7, 1.8, and 1.9 on pages 8-10 of the ABOP download. See Framework.jar.
  3. Create a new Drawable class with the name of LSystem (LSystem documentation). The animation strategy will be to render the image as a plotting device would, one segment at a time.
  4. Create a Turtle class that encapsulates the properties of the drawing pen manipulated by LSystem's draw() method (Turtle documentation).
  5. (Optional) Feel free to incude an L-System of your own design/creation or even one you've googled. Alternatively, how about an origami version?
  6. Submit your updated Framework source code to handin and have your web page updated by the deadline.

Extra Credit. In response to the interest in an independent project for extra credit, I have assembled five images below for your consideration. If you find an image intriguing you are invited to contact me to work out the specifications and timeline of a possible project.

Dragon Curve: Tesselation Dragon Curve: Morphology Sierpinski Zoom
Newton's Method: f(z)= z5-1 2D Barcode: Data Matrix ?
 
2D Barcodes: Data Matrix. Barcode Generator from IDAutomation.com. GS1 Data Matrix Introduction and Technical Specification. Wikipedia.

KOCH CONSTRUCTIONS: Tilings (Tesselations). We'll use this short week for a particularly creative enhancement to our Framework.

Attempts to cover a plane with shapes is both a fascinating and practical application of geometry. The decorative arts are a rich source of examples of tiling the Euclidean Plane from the ancients to the more modern (Gaudi, Escher). Indeed, one of the greatest geometers of the 20th Century, H. S. M. "Donald" Coxeter, spent most of his career at the University of Toronto (1907-2003) in which he explored tilings of the Hyperbolic Plane among other pursuits. (see TVO's: The Man Who Saved Geometry)

Understandably, shapes that possess symmetrical properties lend themselves easily to tiling. This author highlights four types of symmetries in the plane. By simply translating squares and hexagons, the plane can be completely covered. Triangles require glide reflections (reflection & translation) to accomplish the same feat.

Task.

  1. Run Framework.jar and study the four tilings under the Koch Constructions menu.
  2. Add menu items entitled Snowflake Tiling and Island Tiling under the Koch Constructions menu of your Framework.
  3. Rotational symmetry is inherent within your Triadic Koch Snowflake (6-fold) and Quadratic Koch Island (4-fold) sprites. Exploit this characteristicthrough the use of your Transform2D classes to present a tiling of the entire plane for each selection.
  4. We can never be sure where our interests will lead us. One or more of you may be interested in further investigations combining your coding skills with geometry and topology. One such classic twinning is the Four-Colour Theorem.
Snowflake Tiling Island Tiling Départments Français?

Fractal Framework: Web Support. Complete the web support content for each of your Framework entries up to and including the Triadic Snowflake and Quadratic Island algorithms. Remember, this is a body of work you will want to proudly reflect on in the years to come. The focus of your content should be to explain using your mathematics skills, not merely casually summarize in words. Your readers want to learn! To assist with the Triadic Snowflake, consider completing and summarizing the table to the right for the perimeter and area of the Snowflake.

 

 

 

 

 

 

KOCH CONSTRUCTIONS: Triadic Koch Snowflake and Quadratic Koch Island. With a preliminary understanding of the Cantor Set we are ready to undertake a related set of fascinating structures attributed to Helmut Koch that continued to challenge the conventional notion of Dimension well into the 20th Century. Whereas Cantor simply removed the middle third of a line segment, Koch proposed that it be replaced by two segments of equal length.

Cantor Koch

The bridge from Cantor to Koch can be inferred from the graphic below left, that also highlights the recursive application of each man's strategy. Koch went further. He started with an equilateral triangle (initiator) and recursively applied his replacement strategy (generator) to produce his, now-famous, Koch Snowflake (below right).

Cantor → Koch Koch Snowflake

Now it gets really interesting. Koch's replacement proposal opened the door to a variety of generators, one of which led to the Quadratic Koch Island depicted below.

Island Initiator and Generator Quadratic Koch Island

The iconic Triadic Koch Snowflake and Quadratic Koch Island belong to the set of plane-filling curves or PFCs. The realization of this assignment will result in a third menu in your Fractal Framework devoted to a class of PFCs that we'll refer to as Koch Constructions (there's not enough time in this course to investigate 3D space-filling curves (SFCs) but I'd welcome an email from you someday linking me to your future explorations). Here's what your aiming at in this stage of the project.

Triadic Koch Snowflake Quadratic Koch Island

Task.

  1. As a starting point for this project, consider Exercise P13.15 from last year's text book. Create a project called Koch and drop in the classes, Koch.java, KochComponent.java and KochLine.java. Execute the project and digest the author's design.
  2. Create a new Drawable class by the name of TriadicKoch that encapsulates an ArrayList<Sprite> of size equal to the maximum depth of generation.
  3. A call to Sprite's createData() method (or some similar call) can create an equilateral triangle that can be rotated and scaled into position through appropriate Matrix2D transformations as a generation 0 starting point.
  4. Using an algorithm similar to Horstmann's Koch example above, employ recursive generation strategy to propagate a sequence of Sprites representing the outline of successive generations the the Koch Snowflake.
  5. Koch's draw(BufferedImage img) method can create and fill a Polygon from the respective Sprite data.
  6. Repeat the 4 steps above for the class QuadraticKoch.
  7. (Optional) Design your own generator, implement it, name it, and add it to your menu.

CANTOR SETS (Part 3 of 3): Triadic and Quadric Cantor Strategies. Look at the gif animations below. Execute Framework.jar to see them live. Your previous experience with the Linear Cantor Set would suggest that a recursive removal algorithm could be undertaken to generate these 2D Cantor Sets as well. Although we don't have the time to pursue an investigation of the 3D Cantor Set this year, it may be something you may wish to investigate in the future.

 

Triadic Cantor (depth=7) Quadric Cantor (depth=6)

Task.

  1. Under the Cantor Sets menu, and another item entitled, Triadic.
  2. Implement a new Drawable class entitled TriadicCantor. Its constructor should receive Framework's appDimen object so it knows the dimensions of the BufferedImage it will be drawing to. It will also receive the maximum depth of removal. The animated gif to the right presents a depth of 7. Your constructor should generate a entire collection of subsets to be 'removed' prior to finishing. In this way the draw() method will simply access the require number of levels on each call.
  3. Modify Content's current object to point to an instance of the TriadicCantor. This will make it appear when the applet launches.
  4. Repeat Steps 2 and 3 by implementing the class QuadricCantor.
  5. A premium will be reserved for code that is efficient, clear and well documented. One of the ways this can be accomplished is to make maximum use of the Polygon class and any of the JCF data structures we've studied.
  6. The original triangle has an area. With each recursive stage, area is removed. Two interesting questions to ask yourself then is, "How much area remains at each stage of the deconstruction?", and "Eventually, is all the area removed or is there a limit?". After a few weeks of Calculus you'll be able to formulate a mathematical answer to these questions. Let me know when you get there and we'll discuss it.
CANTOR TERNARY SET (Part 2 of 3): Implementation. In this assignment you are asked to render the Cantor Ternary Set with a strategy invloving the transformation of rectangles of minimal height to represent the line segment intervals.
  1. Add a new menu to the immediate right of Gaskets, entitled Cantor Sets.
  2. Implement a new Drawable class entitled LinearCantor. Its constructor should receive Framework's appDimen object so it knows the dimensions of the BufferedImage it will be drawing to. It will also receive the maximum depth of removal. The animated gif to the right presents a depth of 5.
  3. Modify Content's current object to point to an instance of the LinearCantor. This will make it appear when the applet launches.
  4. After consulting a number of online references for the Cantor Set give careful thought to the design of the data structure to house the intervals (Model) and the manner in which you will render the Model (View) (clear separation of Model and View is critical to effective implementation). You are strongly encouraged to add your Transform2DTest project to Framework's Build Path. Your Point2D, Matrix2D and Transform2D classes are terrific support for this and upcoming projects.
  5. Display the Set to depth of at least 5 removals.
  6. A premium will be reserved for code that is efficient, clear and well documented.
Note. Feel free to execute this version of Framework.jar. Although it is not required, a design that places calls to createNewImage()and repaint() within the run() method of a Thread enhances your viewers understanding the dynamic development of the fractal sets.
CANTOR (TERNARY) SET (Part 1 of 3): Analysis. The Cantor Set is an appropriate launch point for our consideration of fractal and topological dimension. A recursive (or iterative) algorithm removes an open third of each segment at each stage of propagation. For this reason, the Cantor Set is also known as the ternary or middle third Set. Here is a link to Wolfram's (Mathematica) animation.

  1. You are asked to research the Cantor Set using as many references as you require to explain the propagation process in your own words and identify one or more of its remarkable properties.
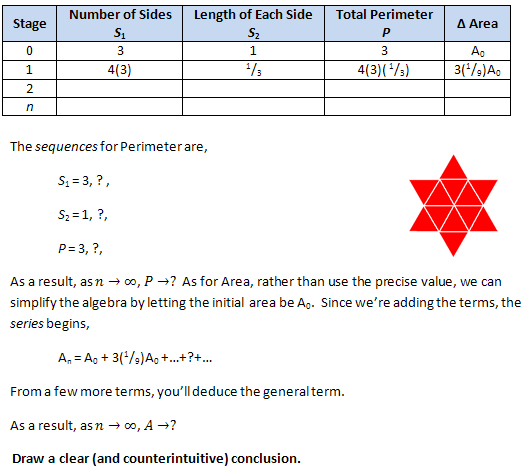
  2. On your ICS4U home page that contains your Fractal Framework Applet, code an HTML table similar to the one below (do not simply add this graphic) that presents a quantitative analysis of the stages of the Cantor propagation. W3Schools: Images, Tables
  3. State the Fractal (Hausdorff) dimension of the Cantor Set accompanied by an explanation.

  4. The original line segment has a length. With each recursive stage, length is removed. The interesting question to ask yourself then is, "Eventually, is all the length removed or is there a limit?"

Note: A premium will be placed on the inclusion of graphics of properly formatted mathematics captured from Word's Equation Editor or some such typesetter.

Map<Friend,Friend>: Social Network. Part 2 of 2. TBA.

Map<Friend,Friend>: Social Network. Part 1 of 2. I have come to the conclusion that ACES are spending too much time programming and not enough time socializing. To resolve this situation, I have assigned each student a friend. Friendship is one-way. That is, if Allan is assigned to be Jiashi's friend, Allan must be friendly to Jiashi, but Jiashi is not required to reciprocate. Every student is assigned exactly one friend. Sometimes, a circle of friends occurs. For example, if Allan is assigned Jiashi, Jiashi is assigned to Juhan, Juhan is assigned Hunter, and Hunter assigned to Allan, we have a circle of 4 friends containing Allan, Jiashi, Juhan, and Hunter. In the circle, we can say that Allan has a Bacon Number of 0 from Jiashi, of 1 from Juhan, of 2 from Hunter (and of 3 from himself).

Task. From a TreeMap of friends, determine whether two students are in the same circle of friends, and if so, state the Bacon Number of the first from the second.

  1. Create a project called Network and a driver class of the same name that encapsulates a TreeMap<Friend,Friend> Collection.
  2. Create an inner Friend class along the design of the UML
  3. Network's main method reads in the mappings from the text file, Friends.txt, and constructs the map.
  4. Implement the recursive Network method, 
    /**
 * This recursive method displays the sequence of Friends 
 * from x to y and returns the corresponding Bacon Number of x -> y.
 */
 private int baconNumber (Friend x, Friend f, Friend y)
  5. Each run of Network will randomly select two Friends (keys) x and y, from the map and either determine the Bacon Number from x to y or state that they are in a Different Circle.

Sample Input:

Juhan Hunter
Jack Allan
Hunter Reuben
Allan Jiashi
Jiashi Juhan
Reuben Jack
Arshia Lakshay
Adrian Michael
Lakshay Adrian
Michael Arshia

Output 1:
Juhan->Hunter
Juhan->Hunter
Bacon Number: 0

Output 2:
Allan->Jack
Allan->Jiashi->Juhan->Hunter->Reuben->Jack
Bacon Number: 4

Output 3:
Jack->Lakshay
Jack->Allan->Jiashi->Juhan->Hunter->Reuben
Bacon Number: Different Circle

Output 4:
Arshia->Arshia
Arshia->Lakshay->Adrian->Michael->Arshia
Bacon Number: 3

IP Address Map. Part 1. The Domain Name System (DNS) is essentially a map that associates an English-like string (URL) with a 4-octet numerical sequence called an IP Address used by networking components for the purpose of locating hardware devices around the globe. For example, here are a few String→IP Address (Key→Value) pairs associated with our school (and a few that aren't).
String (Key) IP Address (Value)
4-octet dotted decimal long
rsgc.on.ca
216.223.144.215
3638530263
ssd.rsgc.on.ca
216.223.144.214
3638530262
gallery.rsgc.on.ca
216.223.144.213
3638530261
edge.rsgc.on.ca
216.223.144.212
3638530260
google.com
74.125.227.19
1249764115
facebook.com
69.63.181.12
1161803020

Feel free to use this IP Address Lookup utility to determine additional IP Addresses.

Task.

  1. Create a Java project entitled DNS and an associated driver that declares a class field of the type: TreeMap<String,IPAddress>.
  2. Create an inner class called IPAddress that accepts the 4-octet String as the only parameter to its constructor. Include a toString() method that echoes the 4-octet String.
  3. Create a text file called Mappings.txt with the (Key,Value) pairs from the table above and a few more of your choosing (one pair per line, separated by at least one space). Use String's split(regex) method to separate the Key from the Value.
  4. In the main method of DNS, read the pairs from Mappings.txt and populate your TreeMap.
  5. After all the Key→Value pairs have been read in display the map to the console window.
  6. Solicit a URL String from your user and use your map to find and display the associated 4-octet IP Address. If the URL is not in your map, display, 'Unknown'.

Part 2. The 4-octet, dotted-decimal IP Address is typically converted to a single 32-bit number as indicated in the graphic to the right. A range of numbers is assigned to various countries.

Task.

  1. Add statements to your IPAddress constructor that will convert the 4-octet String to type long, ideally in a single expression. Use the << operator to maximize the efficiency of the conversion.
  2. The file ip-to-country.csv contains a fairly up-to-date list (Dec 2010) of the range of addresses and their corresponding country information. Examine the structure of this file and using your knowledge of collections, and the big-O of their algorithms, settle on a preferred data structure that can be used to determine the country information from a given long IPAddress. Implement your design and be prepared to justify it to your peers next class.
  3. Modify the statements in your DNS project so that country associated with the URL is also displayed alongside of the dotted-decimal address.

Framework: Runnable Upgrade. I regret not requiring that the Content object be Runnable from the outset. The benefit to your viewers of seeing the evolution of your various Drawable graphics is substantial. I have gone back over previous (and proposed) projects and added the Runnable interface to the Content class. Take a look through the various menu items and see the impact of this enhancement. Please find the time as soon as possible to make this upgrade. Be sure to remount a new version of Framework.jar on your ICS4U site.

Tasks.

  1. Add a call to startThread() from each level of Framework's actionPerformed(ActionEvent ev) method, as in,

    The body of this new Content method is simply,

  2. The body of Content's run() method could look something like the example below that does little more that encapsulate the familiar calls to createNewImage() and repaint().

    Note. Since not all classes you'll want to animate will require the same sleep delay, you may wish to implement a setSleep(int s) method within Content to customize the speed of animation for specific renderings.
  3. As you can see from the body of the run() method above, you'll need to add an abstract finished() method to the Drawable interface and provide a body for each class that implements the Drawable interface.
TreeSet<Account>: AccountTest. (In class) There is a practical need to generate unique account numbers for clients over a range of values.

Task. Develop the class, Account, as defined by adjacent UML diagram. Start with the driver, AccountTest.java and add statements that will generate the output contained in AccountTest.txt. You can infer from the output, the logic required.

The idea is to populate a TreeSet<Account> with the requested number Accounts constructed with unique, n-digit integers (converted to Strings). Note. Recall the add() method returns boolean.

The TreeNode class (defined on page 582) can serve as a versatile base class for your Account class (and future project classes).

PriorityQueue: Too Many Assignments. (The text of this assignment has been adapted from one that appeared on a website for UofT's CSC148 course in the summer of 2010).

You will be implementing a tool to help you decide which homework assignment to work on. Homework assignments have a name and a list of parts. Each part has the following attributes: what they're worth (let's call this value) and the time to complete (let's call this time_complete). Homework assignments don't have due dates; the only goal is to prioritize the order you work on assignments.

You will use a priority queue to determine which assignment to work on. You can only work on the smallest numbered part of an assignment (you cannot work on part 2 until you have completed part 1, and you cannot work on part 3 until you have completed both parts 1 and 2).

The priority of each assignment is the priority of the smallest numbered part that you haven't completed yet. The priority of each part is calculated by dividing value by time_complete. The next homework assignment to work on will be the one with the highest priority. If two items have the same priority, the one that was added to the queue first should be viewed as having higher priority. The operations on the priority queue are as follows:

An assignment gets created with a name. Then parts are added to it. Parts are added in order, so the first call to add_part will be named part 1, the second part 2 and so on. Note that you are NOT responsible for ensuring that all parts in the assignment add up to a specific number.
Your Classes
You will create at least the following classes:

Here are some examples. Here are the above examples in [Python] code. At a minimum, your implementation should pass these tests. Note that these are not the only tests that we will run on your code. So you must do your own testing to ensure that your code is robust.

ACES Task.

  1. You're going to use your Java skills to duplicate this assignment as closely as possible, in spirit. Wherever necessary however, you are to revert to Java preferences for elements such as naming converntion for identifiers and method names for Collections.
  2. Create a project called Scheduler, and translate the Python code into this driver's code. Create inner classses for Assignment, Part and Decider.
  3. Attach Scheduler.java to an email to handin by the deadline under the Subject Line: Too Many Assignments.
GASKETS: Apollonian Gasket. You are not required to code the Apollonian Gasket but you may find it's construction compelling.
GASKETS: Pascal's Carpet. We return to Pascal's Triangle, yet again, to reveal another one of its secrets. Look at the Triangle again, focussing on groups of adjacent even numbers. The resulting image should be surprisingly familiar.

Task.

  1. Under the Gaskets menu, add another item entitled Pascal's Carpet.
  2. Add the Drawable class entitled PascalsCarpet whose draw() method plots a pixel for only the odd terms. Since you are plotting only pixels you can generate as many rows of Pascal's Triangle as the height of your applet. Be careful to maintain no worse than an O(n2) algorithm.
  3. Your triangle should fill the entire panel as an equilateral triangle rather than the default right triangle. Only a litte more thinking required here.
  4. Update your home page (updated applet and jar link).
  5. Submit your source code to handin by the deadline under the Subject: Pascal's Carpet.

GASKETS: The Chaos Game. Familiarize yourself with this recreational version of the Chaos Game.

Tasks.

  1. Familiarize yourself with MouseDemo.jar and its source code. The UML above gives you some idea of the enhancements for this mouse accommodation.
  2. Add a new JMenuItem (after Pascal's Numbers) to The Chaos Game
  3. Design and implement the Drawable class, ChaosGame, that, after three mouse clicks from the user, will display a 100,000+ points according to the conditions of the Chaos Game.
  4. Remount your Framework applet and jar link and provide an additional link from your ICS4U Home Page to the Chaos Game.
  5. Submit your source code to handin by the deadline under the Subject Line: The Chaos Game.
Framework. Since many of the investigations ahead of us are graphic, a dual graphic framework (application/applet) that would permit your users to select from your various undertakings would make a impressive portfolio for the years ahead. Create a project called Framework and drop in this source code.

Tasks.

  1. Review the UML diagram above for the Framework code.
  2. Generate the javadoc and review the pages.
  3. Run the code as an application, selecting the only menu item available, and then close the window.
  4. Repeat the execution, this time launching it as an applet (make sure to set the width and height to 500 in the Parameters Tab of the Run Configuration dialog.
  5. Finally, review the code, familiarizing yourself with all aspects.

GASKETS: Pascal's Numbers. You explored Pascal's Triangle earlier in the course so it won't be too much difficulty adapting its generation yet again, this time for a graphics context. Complete the body of PascalsNumbers' draw() method to display the required number of rows onto its img object. Generate the values using the most efficient Big-O strategy you can implement and be sure to enable the characters to line up in columns. Finally, add Framework to your home page as both an executable jar and an applet to confirm. Submit your source code to handin.

Simulation: Queues. An interesting ad on TV these days is a boast by Lowe's that if a checkout line grows longer than 3 customers, they'll open a new one. As an expert in the field of Management Science, you have been contracted to determine how realistic this claim is. With the holiday season fast-approaching, a few store managers are worried that they may not have the staff to honour this initiative.

A checkout line is a FIFO structure, we'll model with a Queue (LinkedList<E>) object. For the sake of our simulation, let's assume Big Box stores are constructed these days with a maximum of 10 check-outs. In Lowe's case, they always have one checkout open, and others opening as required to meet their boast.

In this project, you are to run a one-day simulation of the checkout station(s), monitoring and reporting the day's activities, and summarizing the results at the end of the day. Here's the output from a sample run.

Task. From the data given to you, customers (instances of the Customer Class) arrive in random intervals of 1 to 4 minutes. Also, each customer is serviced in random integer intervals of 1 to 4 minutes. Obviously, the rates need to be balanced for line lengths to remain manageable. If the average arrival time is larger than the average service rate, the queue will simply continue to grow. Even with balanced rates, randomness can still cause long lines.

Run a simulation for a 12-hour day (720 minutes). Here's a rough guideline for each minute of the day:

Maintain the necessary data so that at the end of the simulation, the program summarizes results for the following:

Final Recommendations,

Using the driver Simulation.java develop and submit the BigBox.java and Customer.java class files that will yield output similar to the above.

MODELING IN R2: PART 3. Animation2D. In this final instalment, we integrate the foundation classes you have developed over the previous two projects to demonstrate the applicability of matrix-defined transformations to simple, but compelling, two-dimensional animations.

Task. Create the project, Animation2D, and add this driver. Configure your build path to include your Transform2D classes to access Transform2D, Matrix2D, Point2DList, and Point2D. This is the best of both worlds, since we're only keeping 'one set of books', so to speak. Look over the driver code. The general idea is to transform a Sprite object(s) to the coordinates for the next frame within the updateScene() method. The loop in the run() method will then call the paintPanel() method in which you can retrieve your Sprite's updated coordinates to populate a Polygon object. This polygon object can be added to the scene through a call to Graphic2D's draw() method.

Here's the full Javadoc. I've created a very elementary example to the right. Considering your vast exposure to gaming animation, I know you'll take your effort to a whole new level.

Note. The classes in this project reflect a strong hierarchical design. I would expect your code to capitalize on the strength of this design; writing tight, efficient carefully-crafted statements that fully exploit the cascading nature of the respective class methods.

Submission. Attach your Animation2D and Sprite classes (and any other previous classes that have been enhanced) to an email to handin with the Subject: Animation2D by the deadline.

2010-2011 Results: Click on each image to run the executable jar.

MODELING IN R2: PART 2. Transform2D. In this second instalment, you are asked to created a project called Transform2DTest, using the driver, Transform2DTest.java. Add the class file Point2DList.java and implement the supporting Point2D. Configure your Transform2D project to refer to your Matrix2D class found within your Matrix2DTest Project, as I will when I evaluate your work. Note that this is a far safer project design as you are not maintaining two or more versions of the class.

Task. Write the two class files, Transform2D.java and Point2D.java, that will work seamlessly with the other existing classes to produce this output. I have prepared the documentation that will guide your effort.

Please attach the following separate class files: Transform2D and Point2D, to an email to handin with the Subject: Transform2D by the deadline.

MODELING IN R2: PART 1. Matrix2D. In this 3-part project (due Saturday November 6), you are introduced to the matrix algebra of transformational geometry leading to a creative graphic animation. Below are the submissions of last years' ACES. Check out more samples from ACES of previous years:

PART 1. Matrix2D. Develop a set of cascading set of constructors and required methods for the class, Matrix2D that can be used with the driver Matrix2DTest.java to produce this output.

Notes

  1. Develop a UML class diagram for the Matrix2D class, save it as a .gif to the image folder of your FC Web Publishing area, and reference it in the class javadoc.
  2. Make every attempt to maximize the use of a minimal set of methods.
  3. Minimize the dependency of your code on direct references to the only instance field, matrix.

Reverse Polish Notation. In this assignment, you are to evaluate a simple arithmetic expression, supplied in postfix notation (also called Reverse Polish Notation). For example, consider the standard infix notation, 2*(3+4). Written as an RPN expression, it would appear as 234+*.

Task. Develop the class, Expression, that can be used with the driver, ExpressionTest.java to generate the output below.

(In-Class) Recursive Parentheses Matching. The example method on page 480 offers an iterative solution to confirming whether a String consists of correctly matched parentheses. It would be more interesting if it were recursive. Create a project called BracketTest and drop in this driver class.

The class contains an instance field of type, Stack<Character> that can be exploited from within the recursive matchParens(Strin expr, int i) method.

The predicate methods, isOpenBracket(char ch) and isCloseBracket(char ch) can be used to write cleaner, more readable code within your matchParens method.

Output should appear as follows,

Combination Lock. Since Java's LinkedList<E> class maintains this data structure as a doubly-linked list, users can traverse it forward and backward with the help of a ListIterator<E> object. Create the project LockTest and a driver that manipulates the class, Lock, defined by the UML specification below. You will need to complete the conditions in each of the while statements in the driver for the project to work correctly.

With a correct implementation of the Lock class initialized with the combination, 21-32-34, your driver will generate the following output,

Three Recursive Classics. Given what lies ahead for students with your academic ability, it is appropriate to confront some of the classic recursive problems in our field at this time. Whereas countless internet sites offer ready-to-go solutions to these gems, conquering these problems on your own rewards you with a sense of scholastic satisfaction unlike few others. More importantly, undertaking deep analysis of simple problems builds the essential problem-solving framework you'll need to tackle more advanced challenges that lay ahead for which solutions may not be readily available.

We have determined from previous efforts that a successful recursive solution to a problem defined as a function of n, lies in the discovery of a two-part, piecewise solution consisting of the base case (typically, but not limited to, n=1) and the inductive case (a simpler problem expressed in terms of n-1). For each of the problems below, challenge yourself to find this piecewise solution with pencil and paper. Once you do, your coded solution will likely yield the correct result on the first run.

1. The Euclidean Algorithm. At the very least, all natural numbers share a common factor of 1. Euclid discovered the property that the greatest common divisor of two integers a and b, gcd(a,b), not both of which are zero, is the largest positive integer that divides both a and b. The Euclidean algorithm for finding this greatest common denominator of a and b is as follows:

Divide a and b to obtain the integer quotient q and the remainder r, so that a=qb+r (if r=0, gcd(a,b)=b). Then gcd(a,b)=gcd(b,r). Replace a and b with b and r and repeat this procedure. Because the remainders are decreasing, eventually a remainder of 0 will result. The last nonzero remainder is gcd(a,b). For example, 

	1260 = 198⋅6+72		GCD(1260,198) = GCD(198,72)
	 198 = 72⋅2+54		              = GCD(72,54)
	  72 = 54⋅1+18		              = GCD(54,18)
	  54 = 18⋅3+0		              = 18
(Note: If either a or b is negative, replace them with their absolute values in this algorithm.)

Develop the driver class RecursiveClassics that will solicit any two natural numbers (use JOptionPane's showInputDialog method). A call to your gcd(a,b) method will return the greatest common divisor of the two parameters. Finally, identify the Big-O of this method in the javadoc comment of the method.

2. Towers of Hanoi. Legend has it that a Brahman monk was charged with the task of moving 64 golden disks (of increasing diameter from top to bottom) from one post to another post. The two stipulations placed on the task were that only one disk could be moved at a time, and no disk of greater diameter could rest on top of one with of lesser diameter. A third post is always available for temporary placement. Task. You are display the moves necessary to complete the task. Code the recursive method below into your NumericalMethods class,

/*********************************************************************
 * This method displays the specific moves necessary to move n rings *
 * from the source post to the destination post using a temporary    *
 * post. The big-O of this task is O(?)                              *
 * @param n the number of disks                                      *
 * @param src the name of the source post                            *
 * @param dst the name of the destination post                       *
 * @param tmp the name of the temporary post                         *
 *********************************************************************/
 public static void showMoves(int n, char src, char dst, char tmp)

Add statements to your RecursiveClassics driver that will solicit the number of disks to be moved and a subsequent call the showMoves method as follows,

showMoves(n,'A','B','C');

For n=3, your output should read,

  Move A to B
  Move A to C
  Move B to C
  Move A to B
  Move C to A
  Move C to B
  Move A to B

3. Permutations. Last week we reviewed how the leaves of a binary decision tree could contain each of the permutations of a set consisting of n unique elements. The example in our text confirmed that a set of 3 unique elements yielded 3! or 6 leaves. In this exercise you will display all permutations of the characters of a given String. Task. You are to display all permutations of the string submitted by a user. Add the method below to your NumericalMethods class,

/*********************************************************************
 * This method displays all permutations of the StringBuffer str     *
 * The big-O of this task is O(?)                                    *
 * @param str the String whose permutations are to be displayed      *
 * @param n the length of the substring of str under consideration   *
 *********************************************************************/
 public static void permutations(StringBuffer str, int n)

Add statements to your RecursiveClassics driver that will solicit the string, str, to be permuted and a subsequent call to the permutations method as follows,

permutations( new StringBuffer(str), str.length());

For the string "ABC" the output shoud read,

BCA
CBA
CAB
ACB
BAC
ABC
Insight into a recursive design. For the string "ABC" there are 3! or 6 permutations. These appear as leaves in the tree below. At each stage of n, a loop is engaged that swaps the last character in the string will all others, calling the method each time with a reduced n, and swapping them back upon its return.

 

Binomial Theorem. A deep understanding of the Binomial Theorem will prove useful to you in the months and years ahead. You'll undertake a computational investigation of the Binomial Theorem in this two-part project. Note: For our purposes, we'll favour recursive strategies over iterative implementations strictly for the experience. Here's a reasonably compact definition of the Binomial Theorem,
(BT-1)

Application of (1) yields familiar binomial expansions,
(BT-2)

Part 1. Combinatorics. Consider the following definition from the field of Combinatorics,
(BT-3)

The left side of (3) is read as n choose r and represents the number of combinations of n one can make, choosing r items at a time (the last two expressions are different ways of expressing the same concept). As can be seen, the determination of this integer result relies on factorials. For example, assuming 5 students show up for class and I need to choose 2 students to go down to Bloor and pickup the sushi order I placed for lunch. How many ways can the pair of students be chosen? There are 10 such combinations as can be seen below.
(BT-4)

  1. Create a project called, BinomialTheorem that exercises the methods in your static NumericalMethods class below. Create a static NumericalMethods class (unless we did so last year), and add the following methods, 
    2. /***************************************************************************
* This method determines the value of n!, recursively                      *
* Precondition: n>=0                                                       *
* Postcondition: the method returns the value of n!                        *
* @param n the whole number for which the factorial is to be determined    *
****************************************************************************
public int factorial(int n)

/****************************************************************************
* This method returns the number of combinations that can be expected given *
* n items, taken r at a time. This does not need to be recursive.           *
* Precondition: n>=0, 0<=r<=n                                               *
* Postcondition: the method returns the value of nCr                        *
* @param n the number of items from which combinations are taken, n>=0      *
* @param r the number of items taken, 0<=r<=n                               *
*****************************************************************************
public int choose(int n, int r)
  2. Now you will display Pascal's Triangle. Add the non-recursive method below to your BinomialTheorem driver, 
    /**********************************************************************
* This  method displays a number of rows of Pascal's Triangle         *
    * Precondition: rows>0                                                *
* Postcondition: the method displays the requested number of rows of  *
*                Pascal's Triangle. It relies on the choose method    *
* @param rows the number of rows to be displayed                      *
***********************************************************************
public static void pascalsTriangle(int rows)

Finally, indicate the Big-O of each of the three methods above in their respective javadoc comment.

Part 2. Probabilities. In Part 1, each element in Pascal's Triangle was determined through the use of the non-recursive definition in BT-3.

  1. Using pencil and paper, develop a recursive piecewise definition for pascal(n,r) (the term in Pascal's Triangle at the n'th row, r'th column).
  2. Implement your definition from a. through the following method, add it to your static NumericalMethods class. Add the Big-O of this method to the javadoc comment. 
    /**********************************************************************
* This method recursively determines the element of Pascal's Triangle *
* in the nth row, rth column.                                         *
* Precondition: n>=0, 0<=r<=n                                         *
* Postcondition: the method return the element of Pascal's Triangle   *
*                in the nth row, rth column                           *
* @param n the row number                                             *
* @param r the column number                                          *
***********************************************************************
public static int pascal(int n, int r)
  3. To complete this initial look at the Binomial Theorem, add the following two methods to your BinomialTheorem driver and include code soliciting appropriate input from the user.
    4. /***************************************************************************
* This method returns the String representation of the r'th term of the    *
* Binomial Theorem of (a+b)^n                                              *
* Precondition: a, b the String equivalents of the binomial's terms        *
*	              n>=0, 0<=r<=n                                        *
* Postcondition:the method returns the String representation of the r'th   *
*	              term of the expansion of (a+b)^n.                    *
* @param a the first term in the binomial (a+b)                            *
* @param b the second term in the binomial (a+b)                           *
* @param n the degree of the binomial expansion                            *
* @param r the required term in the binomial expansion, 0<=r<=n            *
****************************************************************************
public String binomialTerm (String a, String b, int n, int r)


/***************************************************************************
* This method returns the full binomial expansion of (a+b)^n as a String   *
* Precondition: a, b the String equivalents of the binomial's terms, n>=0  *
* Postcondition:the method returns the String representation of the        *
*                expansion of (a+b)^n                                      *
* @param a the first term in the binomial (a+b)                            *
* @param b the second term in the binomial (a+b)                           *
* @param n the degree of the binomial expansion                            *
****************************************************************************
public String binomialExpansion (String a, String b, int n)

The Golden Ratio, φ. In class last Wednesday we investigated the relationship between the sequence defined by the quotients of successive terms of the Fibonacci sequence and the Golden Ratio, φ. This can be expressed as,

(GR-1)

A compelling topic in pure mathematics is Continued Fractions. The essential idea is that the deeper the evaluation of these expressions, the better the approximation is to the ultimate irrational target, or what we prefer to call it in Calculus, the limit. The programmatic evaluation of these expressions is a good fit with your understanding of recursive methods. Here is one example of the continued fraction for the Golden Ratio.

(GR-2)

The limit of both of these sequences is φ.

Task. Develop a java project called GoldenRatio, the output of which will allow the viewer to confirm that both sequences (1) and (2) converge on φ. You will maximize your use of recursive methods, but beyond that, the design of the classes and methods are yours to decide based on our efforts last year. Beyond the correct answer, my evaluation of your submission will focus on the elements of good programming: class and method design, efficient implementation, strong documentation and highly intuitive output. Finally, keep in mind the following,

  1. Both strategies incorporate recursion to determine their n'th approximations to the Golden Ratio.
  2. The n'th approximation of each strategy are identical (i.e. grFib(1) and grCF(1) are 1, grFib(2) and grCF(2) are 2, and so on...)
  3. Recursive methods are elegantly (and deceptively) simple.

Palindrome. A palindrome is a String of characters that reads the same forwards as backwards. Words like racecar and Madam are palindromes. A phrase like "Madam, in Eden, I'm Adam" is also a palindrome if we eliminate the punctuation and spaces. Your task is to develop software that will verify whether or not an entered phrase is palindromic. Run the executable jar file Palindrome.jar I've created as a model for your own implementation.

Project Expectations

  1. Name the project, Palindrome, and create a driver by the same name that uses JOptionPane's showInputDialog and showMessageDialog methods to communicate with your users.
  2. Create the class, Phrase, that encapsulates the String entered for testing by the user, and implements methods required by the adjacent UML.
  3. The purpose of the preProcess method is to remove punctuation and whitespace from the entered String.
  4. The reverse method is to be recursive.
  5. You are expected to make good use of the available methods offered by the String class.
  6. Full documentation is expected.
  7. Attach Palindrome.java and Phrase.java to an email to handin by the deadline.

Fibonacci.

  1. The first two terms of the fibonacci sequence are defined as t1=t2=1. All remaining terms are defined as the sum of the previous 2 terms.
  1. Develop the Java method public int fib (int n) that iteratively determines and returns the nth term of the fibonacci sequence. What is the Big-O of this implementation?
  2. Write a piecewise definition of the nth term of the fibonacci sequence, tn, in a recursive style similar (1) below. Develop the Java method public int fib (int n) that exercises this definition. What is the Big-O of this implementation?
  3. Is there a way to determine tn in O(1) without using a lookup table?

Improved Power Method. The complexity of versions 1 and 2 of the power function below (iteratively and recursively) is O(n). Can we do better? Consider the following strategy,

 

  1. Explain this algorithm.
  2. What is the Big-O of this algorithm?
  3. Write down the piecewise definition requested
  4. Code the algorithm into the method public int powerImproved(int x, int n)

Power. It is virtually impossible to provide practical programming solutions to a variety of complex problems without recursion. As such, it is an indispensable programming strategy. Having said this, you'll have to decide when it's warranted. Successful implementation of a recursive solution depends on your ability to define a recursive solution on paper. For example, the power function, xn can be defined non-recursively as,

xn= x×x×x×...×x (n times)

Defined recursively, we write,

(P-1)

From (1), the implementation is straightforward. Successful recursive solutions arise from the programmer being able to express a definition similar to (1) for each new problem, that includes both the general inductive substitution expression and a basis or stopping condition.

  1. Develop the Java method public int power(int x, int n) that determines the value of xn, iteratively, and returns the value of the expression. What is the Big-O of this implementation?
  2. Develop a second version of public int power(int x, int n) that determines the value of xn, recursively, and returns the value of the expression. What is the Big-O of this implementation?
  3. Develop a third version of public int pow2(int n) that computes the value of 2n with a running time of O(1).