2012-2013 ICS3U SOFTWARE ENGINEERING
TASKS |
TASK 'CHALLENGE' RATING (offered
to assist you with project management strategies) |
||
Routine |
Typically some deep thinking required,
but not necessarily a lot of coding. |
|
Hard |
Likely involves either a multiplicity of new concepts
and/or new mathematical concepts or algorithms. |
|
Really Hard |
Start immediately, think
hard, employ a stepwise refinement strategy and post concerns
as required. |
|

![]() The Game of Life 2. As a permanent reminder of your recent coding of the Game of Life, you will revisit your Evil Genius soldering skills by assembling the Game of Life v1.3 Kit from Adafruit.
The Game of Life 2. As a permanent reminder of your recent coding of the Game of Life, you will revisit your Evil Genius soldering skills by assembling the Game of Life v1.3 Kit from Adafruit.
Follow the tutorial carefully throughout the week and leave your working system on my desk before you leave this Friday.
![]() The Game of Life. John Conway introduced the world to one of the most studied algorithms within the Cellular Automata family in the October 1970 issue of Scientific American. Read Wikipedia's explanation of the simple rules for propagation. Explore the game through either or both of the Explore links on the course page. Give yourself time to enjoy how such an elegantly simple set of rules can produce such fascinating outcomes. In the applet to the right, I have colour-coded the cells as Birth (green), Survival (red) and Death (black), with Empty cells remaining in the background colour (white) to enable you to better track the evolution of the popluation. Numerous web sites will offer code for the Game of Life so you are asked to stick to my specification.
The Game of Life. John Conway introduced the world to one of the most studied algorithms within the Cellular Automata family in the October 1970 issue of Scientific American. Read Wikipedia's explanation of the simple rules for propagation. Explore the game through either or both of the Explore links on the course page. Give yourself time to enjoy how such an elegantly simple set of rules can produce such fascinating outcomes. In the applet to the right, I have colour-coded the cells as Birth (green), Survival (red) and Death (black), with Empty cells remaining in the background colour (white) to enable you to better track the evolution of the popluation. Numerous web sites will offer code for the Game of Life so you are asked to stick to my specification.
Our Life board is 'played' on a matrix with a base type of Status, an enumerated type. The constants defined within Status will help maintain the precise state of each cell from one generation to the next and help with colour-coding. To ensure ALL cells in the board have exactly 8 neighbours, the border cells on all four sides will maintain the EMPTY status throughout the generations. For the time being, the inital population will be randomly created, using the value of the probability field to assist with the initial population density.
Task.
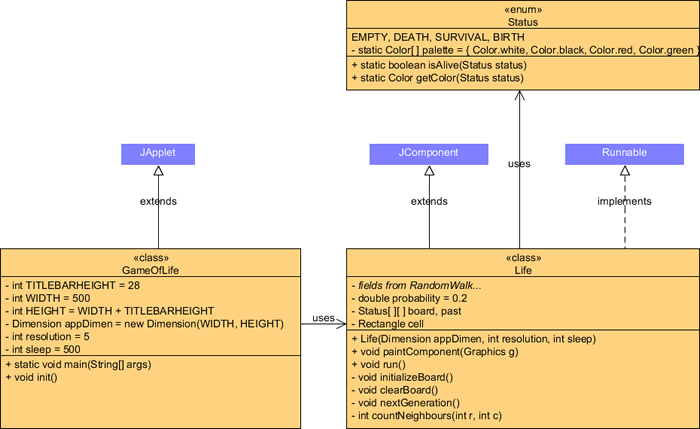
![]() Random Walk. The objective of this in-class task is to establish a platform for graphic animation based on threads. This template will provide a foundation for the remaining assignments in this course.
Random Walk. The objective of this in-class task is to establish a platform for graphic animation based on threads. This template will provide a foundation for the remaining assignments in this course.
Task.
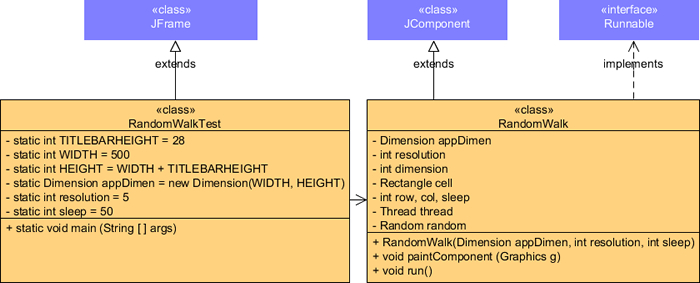
![]() Image Processing. The objective of this in-class task is to appreciate that an understanding of Java's file- and graphics-handling classes can be used to develop some useful image processing utilities.
Image Processing. The objective of this in-class task is to appreciate that an understanding of Java's file- and graphics-handling classes can be used to develop some useful image processing utilities.
![]() Recursive Folder Display. As you are aware, a file within a folder can, itself, be a folder. This a naturally recursive pattern! Your previous experience with recursion will enable you to experience the reward of applying your skill to the task of displaying the full listing of the files within a given folder, complete with an indication of depth, much like the Package Explorer sidebar within Eclipse itself.
Recursive Folder Display. As you are aware, a file within a folder can, itself, be a folder. This a naturally recursive pattern! Your previous experience with recursion will enable you to experience the reward of applying your skill to the task of displaying the full listing of the files within a given folder, complete with an indication of depth, much like the Package Explorer sidebar within Eclipse itself.
 |
 |

![]() Sorts. The
search for a fast, efficient sorting utility has led to
the development of numerous algorithms. Some techniques are easy to understand
and code, but can execute relatively slowly. Others are extremely fast, but
challenging to understand and maintain. In this assignment, you are asked
to compare (time) the
speed of four popular algorithms (Selection, Insertion, Mergesort
and Quicksort). We've developed original code for the first three in class and we implemented the Quicksort from the pseudocode.
Sorts. The
search for a fast, efficient sorting utility has led to
the development of numerous algorithms. Some techniques are easy to understand
and code, but can execute relatively slowly. Others are extremely fast, but
challenging to understand and maintain. In this assignment, you are asked
to compare (time) the
speed of four popular algorithms (Selection, Insertion, Mergesort
and Quicksort). We've developed original code for the first three in class and we implemented the Quicksort from the pseudocode.
Task.
Minor modifications to your SortingAlgorithms code developed in class can be made to produce a tabular comparison of the four algorithms as measured against the same data in a single run. A sample run on my computer yields the results above right (2.4GHz P4). For optimum results you should close all other running processes. For convenience, the code writes the timing results in an Excel-convenient format (space for columns, \n for rows).

Identify the speed of the processor used for your results on the worksheet. Provide an appropriately-labeled graph of the timing results on a separate, full page worksheet, appropriately renamed. Submit both documented SortingAlgorithms.java and Sorts.xls files to handin by the deadline.
![]() (Recursive) Reversal. This past week you were introduced to the concept of recursion as a problem-solving and programming strategy. This exercise will give you another chance to put this technique to work. The task is to develop a method that reverses a String.
(Recursive) Reversal. This past week you were introduced to the concept of recursion as a problem-solving and programming strategy. This exercise will give you another chance to put this technique to work. The task is to develop a method that reverses a String.
Task.

BINGO! This three-part assignment is designed to solidify your array and Arraylist<E> skills.

![]() Bingo1: Bingo Card. Create a project called Bingo1 and add
this driver. As you can see, the driver simply instantiates and
displays an instance of a BingoCard class.
Provide an implementation of the BingoCard class
that follows this
basic UML design. You output should
look similar to the capture below.
Bingo1: Bingo Card. Create a project called Bingo1 and add
this driver. As you can see, the driver simply instantiates and
displays an instance of a BingoCard class.
Provide an implementation of the BingoCard class
that follows this
basic UML design. You output should
look similar to the capture below.

Task. Create a new project entitled, Bingo2 and drop in this driver. Configure Bingo2's Build Path by adding the Project Bingo1 so you only have one version of the BingoCard class. Following this UML diagram, create a BingoPlayer class and implement the enhancements to your BingoCard class. Sample output appears to the right.
Attach Bingo2.java, BingoPlayer.java and BingoCard.java files to an email to handin under the Subject Line: Bingo2.
![]() Bingo3. Bingo
Game. The
final stage of out Bingo Trilogy should be obvious. You are to simulate
a multi-player Bingo
Game. In the past few lessons you have been introduced to Java's ArrayList<E> class
that offers users a suite of methods for the convenient manipulation of arrays.
So, just as the Integer and Double classes
are wrapper classes for ints
and doubles respectively, the ArrayList<E> class
can be thought of as a wrapper for arrays.
Bingo3. Bingo
Game. The
final stage of out Bingo Trilogy should be obvious. You are to simulate
a multi-player Bingo
Game. In the past few lessons you have been introduced to Java's ArrayList<E> class
that offers users a suite of methods for the convenient manipulation of arrays.
So, just as the Integer and Double classes
are wrapper classes for ints
and doubles respectively, the ArrayList<E> class
can be thought of as a wrapper for arrays.
Task. Create a project called Bingo3. Configure Bingo3's Build Path to include your Bingo1 and Bingo2 Projects. Add the text file Players1213.txt to the Bingo3's root folder. Examine the contents of the file. The data file has a number of records that contain two fields each (the player's name and number of cards), separated by a tab. Using much of Bingo2's driver code, create the driver for Bingo3 that populates an ArrayList<BingoPlayer> container with the data from Players1213.txt. Then, undertake a Bingo game in which all players (and all their cards!) participate until a winner is identified. For verification, print out ONLY the winning player(s) and all of his cards. Note: I will use a different Players1213.txt file (with the same field structure) when I evaluate your project.

![]() The Sieve of Eratosthenes. There
is no known efficient procedure for finding prime numbers. A classical, but tedious,
method attributed to Eratosthenes (276 - 196 BC), can be described as follows.
First, write down a list of integers, paired with true values,
The Sieve of Eratosthenes. There
is no known efficient procedure for finding prime numbers. A classical, but tedious,
method attributed to Eratosthenes (276 - 196 BC), can be described as follows.
First, write down a list of integers, paired with true values,
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 T T T T T T T T T T T T T T T T T T T
Then mark all multiples of 2 by switching its true to false,
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 T T F T F T F T F T F T F T F T T T F
Move to the next unmarked number, which in this case is 3, then mark all its multiples:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 T T F T F T F F F T F T F F F T F T F
Continue in this fashion, marking all multiples of the next unmarked number until there are no new unmarked numbers. The numbers which survive this marking process (the Sieve of Eratosthenses) are primes.
Task. Write the class, Sieve, that will implement the Sieve of Eratosthenes and determine the prime numbers from 2 to n-1, where the integer n is determined by the user.
Your program will create an array of length n, initializing all cells to true. Starting with array index 2, (ignore index 0 and index 1), every time an array element is found to be true, loop through the remainder of the array and set to false every element whose index is a multiple of the starting index.
At the end of the implementation, array elements that remain true have an index which is a prime number. Display the prime numbers to the console.
![]() Binomial Theorem. A deep understanding
of
the
Binomial
Theorem
will
prove
useful to you in the months and years ahead. In this project you'll undertake a two-part computational
investigation
of the Binomial Theorem. Here's a reasonably
compact
definition of the Binomial Theorem,
Binomial Theorem. A deep understanding
of
the
Binomial
Theorem
will
prove
useful to you in the months and years ahead. In this project you'll undertake a two-part computational
investigation
of the Binomial Theorem. Here's a reasonably
compact
definition of the Binomial Theorem,
 |
(BT-1) |
Application of (1) yields familiar binomial expansions,
 |
(BT-2) |
Part 1. Combinatorics. Consider the following definition from the field of Combinatorics,
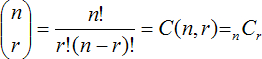 |
(BT-3) |
The left side of (3) is read as n choose r and represents the number of combinations of n distinct items one can make, choosing r of them at a time (the last two expressions in BT-3 are different ways of expressing the same concept). As can be seen, the determination of this integer result relies on factorials. For example, assume 5 students show up for class and I need to choose 2 students to go down to Bloor and pickup the sushi order we placed for lunch. How many ways can the pair of students be chosen? There are 10 such combinations determined as follows,
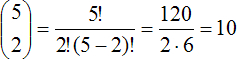 |
(BT-4) |
BinomialTheorem that exercises the
new methods in your static NumericalMethods class. /*************************************************************************** * This method determines the value of n! * * Precondition: n>=0 * * Postcondition: the method returns the value of n! * * @param n the whole number for which the factorial is to be determined * **************************************************************************** public static int factorial(int n) /**************************************************************************** * This method returns the number of combinations that can be expected given * * n items, taken r at a time. This does not need to be recursive. * * Precondition: n>=0, 0<=r<=n * * Postcondition: the method returns the value of nCr * * @param n the number of items from which combinations are taken, n>=0 * * @param r the number of items taken, 0<=r<=n * ***************************************************************************** public static int choose(int n, int r)
 Now
you will display Pascal's Triangle. Add the method below to your BinomialTheorem driver,
Now
you will display Pascal's Triangle. Add the method below to your BinomialTheorem driver,
/********************************************************************** * This method displays a number of rows of Pascal's Triangle *
* Precondition: rows>=0 * * Postcondition: the method displays the requested number of rows of * * Pascal's Triangle. It relies on the choose method * * @param rows the number of rows to be displayed * *********************************************************************** public static void pascalsTriangle(int rows)
![]() Part 2. Binomial Expansion. To complete this year's look at the Binomial Theorem, perform the following,
Part 2. Binomial Expansion. To complete this year's look at the Binomial Theorem, perform the following,
/*************************************************************************** * This method returns the String representation of the r'th term of the * * Binomial Theorem of (a+b)^n * * Precondition: a, b the String equivalents of the binomial's terms * * n>=0, 0<=r<=n * * Postcondition:the method returns the String representation of the r'th * * term of the expansion of (a+b)^n. * * @param a the first term in the binomial (a+b) * * @param b the second term in the binomial (a+b) * * @param n the degree of the binomial expansion * * @param r the required term in the binomial expansion, 0<=r<=n * **************************************************************************** public static String binomialTerm (String a, String b, int n, int r) /*************************************************************************** * This method returns the full binomial expansion of (a+b)^n as a String * * Precondition: a, b the String equivalents of the binomial's terms, n>=0 * * Postcondition:the method returns the String representation of the * * expansion of (a+b)^n * * @param a the first term in the binomial (a+b) * * @param b the second term in the binomial (a+b) * * @param n the degree of the binomial expansion * **************************************************************************** public static String binomialExpansion (String a, String b, int n)

Degrees (d) to Radians (r). The Math class offers two built-in conversion methods, toDegrees(double angrad) and toRadians(double angdeg) for your convenience that implement the following definitions,
![]()
Infinite Series Approximations of the trigonometric functions sin(x) and cos(x), x in R (radians)
![]()
![]()
Task.
public static double sin(double angle)
and
public static double cos(double angle)
based on the two series above that can be used to confirm the accuracy of the built-in methods of the Math class. If your NumericalMethods class works properly, the project will yield the output below (up to 45°, inclusive).
The formulas above suggest another static support method that would be useful.
Pages 222-223 contain eight Programming Exercises considered easy by the author (ExP15_4, ExP15_5, and so on). You are to do them all. Attach fully documented sources files, correctly named, to an email to handin with the Subject: One Star Exercises, by the deadline. I will evaluate one of them at random.

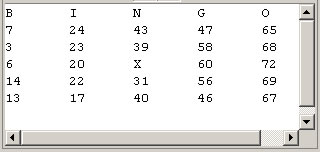
![]() iTunes1. To gain familiarity with boolean operators and expressions, we'll query a database (text file) for data that match specific criteria.
iTunes1. To gain familiarity with boolean operators and expressions, we'll query a database (text file) for data that match specific criteria.
Task.
![]()
Now, construct boolean queries to determine the number of matches for each of the stated criteria below. (Note: You many wish to open Music1.txt in Excel to confirm the data sets your queries produce)
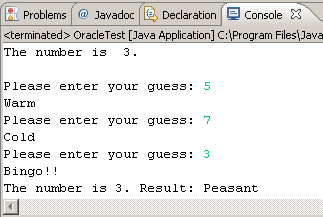
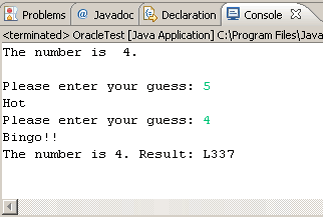
Table 1. Each Guess |
Table 2. Honour |
||
| Guess |
Result |
Number of Guesses |
Level |
exactly |
Bingo!! |
1 |
Jedi |
within 1 |
Hot! |
2 |
L337 |
within 2 |
Warm |
3 |
Peasant |
otherwise |
Cold |
otherwise |
n00b |
 Task.
You are to give the user no more than three attempts
to discover the secret digit. Summarize each game by labeling the player's
outcome
according to Table 2. In addition to printing the label, also display
the secret number for confirmation purposes (not
before as in the two examples). Use as many elements of good
coding conventions and style that
we have discussed and submit OracleTest.java and
Oracle.java to handin by the
deadline.
Task.
You are to give the user no more than three attempts
to discover the secret digit. Summarize each game by labeling the player's
outcome
according to Table 2. In addition to printing the label, also display
the secret number for confirmation purposes (not
before as in the two examples). Use as many elements of good
coding conventions and style that
we have discussed and submit OracleTest.java and
Oracle.java to handin by the
deadline.
 |
 |

![]() Comparing
Objects: Prioritizer. (In class) You are aware that the equality operator
(==)
is
not used to compare the values of two objects. The preferred technique is to
add
the
method, public
int compareTo(Object other)to any class that requires a signed integer
ranking
between the implicit parameter (this)
and the explicit parameter (other)
instances of the
class.
Comparing
Objects: Prioritizer. (In class) You are aware that the equality operator
(==)
is
not used to compare the values of two objects. The preferred technique is to
add
the
method, public
int compareTo(Object other)to any class that requires a signed integer
ranking
between the implicit parameter (this)
and the explicit parameter (other)
instances of the
class.
To assist in the prioritization of assignments that require completion, you are to develop software to tell you what your highest priority task is.


![]() IP
Address. (This assignment will give you practice manipulating numerical
and String data
in the analysis of an Internet Protocol (IP) address) The purpose of this
assignment is to allow the user to enter an IPv4 address in dotted-decimal
form and the software
will convert it to it's binary equivalent (if it is valid). You can restrict
the reasons for an invalid address to either an incorrect number of octets
(there
should be exactly 4) or the value of any given octet is out of range (it
must be between 0 and 255, inclusive). Take a test
drive of the final project. In addition, you are
encouraged to look carefully and the driver's
use of JOptionPane's
input and output dialog boxes. Use these dialogs where appropriate in the
assignments
ahead.
IP
Address. (This assignment will give you practice manipulating numerical
and String data
in the analysis of an Internet Protocol (IP) address) The purpose of this
assignment is to allow the user to enter an IPv4 address in dotted-decimal
form and the software
will convert it to it's binary equivalent (if it is valid). You can restrict
the reasons for an invalid address to either an incorrect number of octets
(there
should be exactly 4) or the value of any given octet is out of range (it
must be between 0 and 255, inclusive). Take a test
drive of the final project. In addition, you are
encouraged to look carefully and the driver's
use of JOptionPane's
input and output dialog boxes. Use these dialogs where appropriate in the
assignments
ahead.
 |
 |
Task.
Suppose the goal is to determine the square root of 20, call it x. Since 16<20<25, we know the answers lies somewhere between 4 and 5, likely closer to 4. In some situations, we could stop here, offering 4 as the square root of 20. But, like any good competition, a better approximation would be impressive. Try this. If we let x=4, Newton suggested,
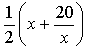
would result in an improved approximation. A quick calculation yields a result of 4.5. Squaring 4.5 produces 20.25. Not bad. Newton's prediction appears to be correct. Ok, from 4 we calculated 4.5. Is this the end of it? Is this the best approximation we can come up with?
Task. Create a project called NewtonTest and drop in this driver. Next, create a static NumericalMethods class and implement (at least) the following two methods,
/**
* sqrt returns an approximation to the square root of the number a,
* given an initial guess of x, using n iterations of Newton's Method
* @param a the radicand
* @param x the initial approximation to the square root of a
* @param n the number of iterations of Newton's Method
*/
public static double sqrt(double a, double x, int n)
and
/**
* sqrt returns THE BEST approximation to the square root of the number a,
* given an initial guess of x, using Newton's Method
* @param a the radicand
* @param x the initial approximation to the square root of a
*/
public static double sqrt(double a, double x)
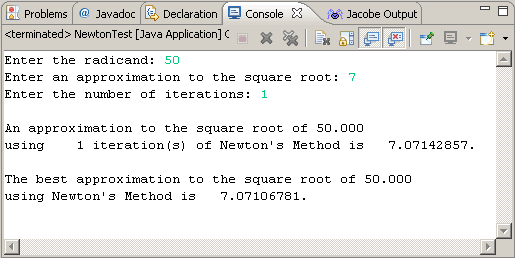
Your code should yield the output below. Submit your NumericalMethods class by the deadline.
![]() Exercise P5.2. Using the UMLet drawing utility, develop an appropriate UML diagram for the Card class
and save it as Card.uxf. Create the project ExP5_2 and add a driver by the same name that accepts user input from the Console window with the help of the Scanner class. The driver processes the input as required and delivers output similar to the sample provided by the problem specification.
Exercise P5.2. Using the UMLet drawing utility, develop an appropriate UML diagram for the Card class
and save it as Card.uxf. Create the project ExP5_2 and add a driver by the same name that accepts user input from the Console window with the help of the Scanner class. The driver processes the input as required and delivers output similar to the sample provided by the problem specification.
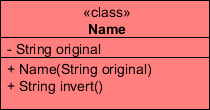
![]() Name.
The dual purpose of this project is to deepen your understanding of methods in the String and the Scanner classes.
Name.
The dual purpose of this project is to deepen your understanding of methods in the String and the Scanner classes.
Task.
 Run the executable jar: NameTester.
Run the executable jar: NameTester.![]() Toyota Logo Revisited. In preparation for next week's larger graphics
application, you are asked to make a few improvements to your previous Toyota
application.
Toyota Logo Revisited. In preparation for next week's larger graphics
application, you are asked to make a few improvements to your previous Toyota
application.
Positioning and Proportion Improvements.
Dimension dim = getSize();Determining the coordinates of the center of the panel is simply a matter of averaging the two measures, while accounting for the height of the title bar. With the center known, constructing the rectangular bounding areas of the three ellipses is straightforward. The only concern you have is allowing enough room at the bottom for the TOYOTA name.
The FontMetrics class of java.awt encapsulates information about the measure (metric) of a given font. Coincidentally, the Graphics2D class has method called getFontMetrics() that returns a FontMetric object that can be manipulated to reveal the bounds of a given String object within the current graphics environment in the form of a Rectangle2D object.
![]()
 Toyota
Logo.
For your first Java2D graphics assignment you are asked to recreate
the
familiar
logo. Create a graphical application called Toyota that
renders the logo to the right as closely as you can. Some of the areas you will
need
to
investigate
include,
Toyota
Logo.
For your first Java2D graphics assignment you are asked to recreate
the
familiar
logo. Create a graphical application called Toyota that
renders the logo to the right as closely as you can. Some of the areas you will
need
to
investigate
include,
Note. An important consideration is the scalability of your rendering. As can be seen from this example, as the frame is resized, the image remains proportional, centered horizontally and scaled to ensure it remains entirely within the panel.
![]() Project 4.1. Consider Project 4.1 as
specified on pp. 179-180.
Project 4.1. Consider Project 4.1 as
specified on pp. 179-180.