You
are familiar with Newton's Method for root finding,| HashMap: Newton's Method |
You
are familiar with Newton's Method for root finding,
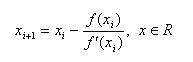
(Did you know he was 19 when he discovered Calculus?) If we replace the real domain with a complex domain, we can examine the behaviour over the Complex (Argand) Plane,
In
this assignment, you will maintain a HashMap of <Key, Value> pairs
to assist in the generation of one of the iconic images from the field of Chaos and Dynamical
Systems. Create the Project, NewtonMap, and drop in the partially completed
driver, NewtonMap.java.
Also include your ComplexNumber class. Suggestion: Check out DeMoivre's
Theorem and
add a pow(int n) method to your ComplexNumber class.
Let's
map
the
Argand
Plane
under
the
influence
of
Newton's
Method
in
its
attempt
to
search for the
roots of the complex function, f(z)=zn-1.
Dieter's map of g(z)=z5-1
appears at the top right. Click to enlarge.
Check out his Nothing
Else Matters zoom video.
Brendan's
map of h(z)=z6-1, using his logarithmic palette,
appears at the
middle right. Click to enlarge.
Editor's
Note: Mathematics
and Computers is a marriage made in heaven.
Task. Develop two classes, Pixel (Key) and Newton (Value) and add (put) these pairs into a HashMap<K,V>. There will be one (Pixel, Newton) pair for each point on screen. After populating the HashMap<Pixel, Newton> you can start the rendering process. Obtain the set of keys from HashMap and iterate over the set to access each associated Newton object. The public access methods of Newton will tell you the number of iterations (and the root if you care to colour code the basins of attraction). Use this information to determine the Color of the pixel. Below are UMLs for a suggested class design. Send me an image when you obtain one and I'll add it to this page.
 |
 |