2005 ICS4M FINAL EXAM-Java

Tuesday, May 31st. 1:00 p.m.

INSTRUCTIONS TO STUDENTS.
  1. Students will complete ONE question from the following TWO alternatives.
  2. This exam counts for 30% of your final mark in this course.
  3. Appropriate coding style and javadoc style documentation are expected.
  4. It is imperative that you name your files exactly as requested. Attach all (and only) the requested files to your email to handin at the end of the exam.
  5. You are allowed to use your textbooks and your ICS4M folder.
  6. You are NOT allowed to access the internet at any time during the exam.
Question 1. RECURSIVE ALGORITHM. (Degree of Difficulty: 1.0)

Solving Linear Systems: Gauss-Siedel

Numerous techniques for solving linear systems involve iteration and recursion. The general idea is that we start with an arbitrary guess for the solution and then we use the equations to progressively improve the solution (very much like Newton’s Method). Here, each equation is solved for one of the unknowns in terms of the remaining ones, then using the initial guess a new solution is obtained which is, in turn, substituted into the equations to yield an improved estimate and so on. We give an example below:

Consider the system Ax = B with,

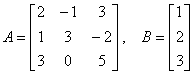
We write:

x1 = ( 1 + x2 ­ 3 * x3) / 2     eq. 1
x2 = ( 2 ­ x1 + 2 * x3 ) / 3    eq. 2
x3 = ( 3 ­ 3 * x1 ) / 5            eq. 3

Now we start with the initial guess [0, 0, 0] and using equation (1) we obtain [ 0.5, 0, 0] . Using this in equation (2) we obtain [ 0.5, 0.5, 0] and using this in equation (3) we obtain [0.5, 0.5, 0.3]. We now go back to equation (1) and obtain [0.3, 0.5, 0.3] repeating this cycle produces the approximations shown (obtained using Excel):

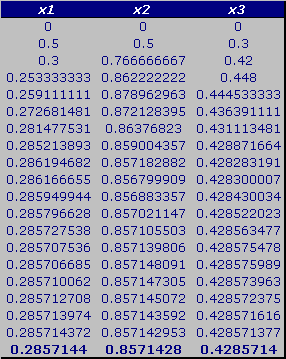
We can check and see that the unknowns converged well to the “exact” values: [ 2 / 7, 6 / 7, 3 / 7 ] .

Task. Add the method,

		  /**
		   * Recursive method implements Gauss-Siedel algorithm
		   * precondition: A, b and x are properly initialized, a unique solution exists.
		   * postocndition: recursive methods returns the unique solution as a 3x1 matrix.
		   * @param A the coefficient matrix
		   * @param b the adjoint matrix
		   * @param x the initial guess
		   */ 
		  public double[][] GaussSiedel (double[][]A, double[][]b, double [][]x)

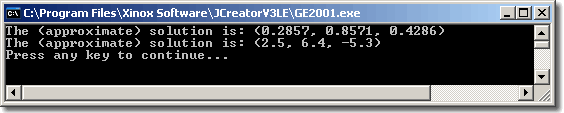
to your NumericalMethods class so that it works with this driver (GaussSiedelTest.java) (unaltered) to produce the following output. You decide on an appropriate basis condition to stop the recursion. Submit NumericalMethods.java to handin.

 
Question 2. CLASSES and DATA STRUCTURES. (Degree of Difficulty:1.05)

Polynomials

Write classes Polynomial and Term that cooperate to store a polynomial such as

as a linked list of terms. A term contains the coefficient and the power of x. For example, the polynomial p can be constructed as,

Polynomial p = new Polynomial();
p.addTerm(-10,0);
p.addTerm(-1,1);
p.addTerm(9,7);
p.addTerm(5,10);
Then, to compute p(x)×p(x), 
Polynomial q = p.multiply(p);
q.print();

Task. Using this driver (PolynomialTest.java), develop and submit your Polynomial and Term classes that yield the following output.