Calculus Project

7. Function.integrate(). As the inverse operation of the well-defined differentiation operation, one would think integration is just as clear cut. However, as you've discovered, if differentiation is a science, integration is an art. In recognition for how advanced your Calculus project is, I'm giving you a lot of latitude with this final segment. Here's what I suggest.

Add the public boolean isIntegrable() predicate method to your Function class that clients can use to confirm whether your application can perform the operation.
This method could first create a String representation of the structure of your yTree. You already have a reportStructure() method that could be used as design model for a more detailed encoding.
This String can now be compared to an array (matrix or map) of patterns you feel you can create integral Expression Trees for.
Pass the index (or encoded integral String) into the array determined in the previous step to the private ENode integrate(int i) method that will construct the integral.

Add methods to your driver to test your new features. Remember to add -1 to your f method (see Step 4) so that clients can evaluate your the integral of your function.

6. Function.differentiate(). This is arguably the most satisfying stage of the project as it doesn't take too much code to open the window to many applications. As you are well aware, there are five derivative 'rules' (Power, Sum, Product, Quotient and Chain). The first four are triggered on the occurrence of ONodes in your Expression Tree, and deserve methods in their name. The Chain Rule is applied as required within the context of the other four rules methods and hence does not require a specific method.

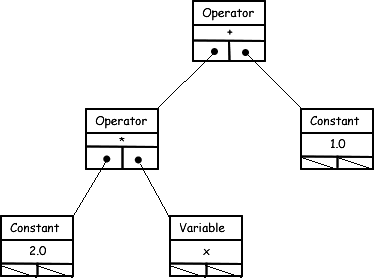
Task. Add the methods suggested by the UML diagram. With the exception of the last method, there should be self-explanatory. In the case of the recursive duplicate() method, deep copies of Expression Trees are required in a number of derivative contexts and I've found that it's quite handy to call on a single method to deliver the copy of the ETree. Once developed, temporarily add the following code to your Function's constructor to test the strength of your methods.

	dyTree = differentiate(yTree);
	//dyTree = simplify(dyTree);
	System.out.println("dyTree Structure: " + reportStructure(1));
	//yp = compose(dyTree);

	d2yTree = differentiate(dyTree);
	//d2yTree = simplify(d2yTree);
	System.out.println("d2yTree Structure: " + reportStructure(2));
	//ydp = compose(d2yTree);

5. Function.expression(). All the groundwork has been laid (expression grammar, qualify(), ENode hierarchy, evaluate(), etc) for the automated creation of the function's expression tree. Add a statement to your Function constructor similar to ENode yTree = expression() and a sequence of methods starting with (non-recursive),

	public ENode expression()

that are used to support and enforce the grammar you created at the beginning of this Project. The package of methods will define a potentially recursive system as defined by your grammar. The sequence of methods

can manipulate a class variable (int) that acts as an index into the qualified String defining your function. You driver should call reportStructure() to confirm the accuracy of what can be called your Recursive Descent Parser.

4. Function.evaluate(). Add the following statement to your Calculus driver,

	System.out.println(f.f(0,1.5));

The intent of the call is to obtain the value of f(1.5). If the Function f is defined as f(x)=2x + 1, and your code is functioning properly, the result should be 4.0. To support the call, add the following methods to your Function class.

	public double f(int which, double x)

and,

	private double evaluate(ENode y)

For the f method, the value of the parameter which is 0 for f(x), 1 for f '(x) and 2 for f ''(x). The f method sets the global value of x and then calls the evaluate method, passing it a reference to the requested function.

3. Function.ENode. The role of the parser (which we have yet to write) will be to construct an expression Tree (ETree). Just as our earlier studies incorporated classes such as ListNode and TreeNode, we need to develop and implement an ENode class design (hierarchy?) whose objects can be used as the fundamental building blocks of our ETree. For example, consider the resultant ETree at the right generated from parsing the expression, 2x+1.

Task. Using the design developed in class add the following to your Calculus Project,

Write the source code for the ENode model
Within the Function constructor, manually construct an ETree for the expression 2x+1.
To your Function class, add the method,
```
 public String reportStructure()
```
that will return the String identifying the infix structure of the ETree:

Constant Operator Variable Operator Constant

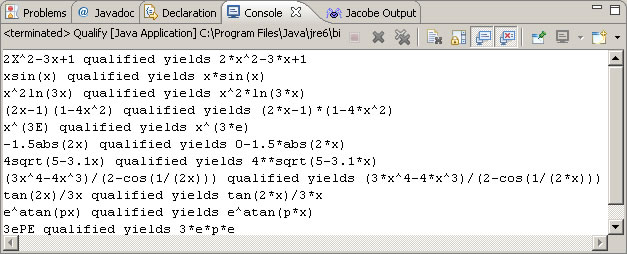
2. Function.qualify(). Create a project called Qualify and use this driver. Develop the private void qualify() method of a Function class that inserts an asterisk in place of all implicit multiplication situations you can think of. Some of you may wish to consider the use of the StringBuffer class and the methods it offers. The output should appear as follows. (e stands for e, and p stands for π). NOTE: From the outset you are encouraged to heavily document your work. It's amazing how quickly you will forget why you coded the way you did.

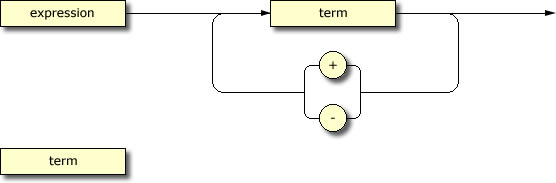
1. Syntax Diagrams for Expression Grammar. Of all the assignments you've been asked to complete over the past four years, you'll remember this one as the most satisfying. For years to come, you will marvel at what you are about to accomplish.

You may not have realized it at the time, but the GIF Decoder project required that you interpret the GIF grammar. The first step in writing my Algebra&Geometry software, was a three-month investment in developing a grammar for the language before I could write an interpreter. So, your first step in developing application software to manipulate mathematical expressions, is to provide an unambiguous grammar for the expressions you hope to interpret.

Using appropriate knowledge and vocabulary, complete a sequence of syntax diagrams for the broadest range of mathematical expressions you have encountered to this point in your development. Here's how the set of rules will start out. You should consider including most (if not all!) of these definitions in your grammar.