2005 ICS3M FINAL EXAM-Java

Friday, June 3th. 1:00 p.m.

INSTRUCTIONS TO STUDENTS.
  1. Students will complete ONE question from the following THREE alternatives.
  2. Superior scores will be reserved for solutions that reflect accuracy, clarity, design, and documentation elements.
  3. It is imperative that you name your files exactly as requested. Attach all (and only) the requested files to your email to handin at the end of the exam.
  4. You are allowed to use your textbook and ICS3M folder.
  5. You are NOT allowed to access the internet at any time during the exam.
Question 1. ALGORITHMIC. (Degree of Difficulty:0.7)

Perimeter of a 2D Polygon

You are familiar with the formula for the distance, d, between two points (x1,y1) and (x2,y2) in mathematics,

If we knew the coordinates of the vertices of a polygon in a cyclic order, we could use this formula to accumulate the lengths of the sides of the polygon and, hence, determine its perimeter.

Task. In this question, you are asked to write the Polygon2D class that can be used with this driver to yield the following output.

Question 2. CLASS DESIGN. (Degree of Difficulty:1.0)

Logic Gates

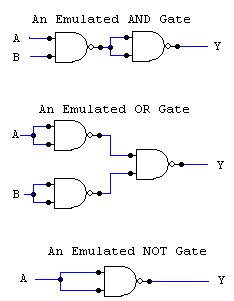Suppose we are working on a 'circuit editor' for an interactive PC-board design application. The class LogicElement is an abstract class that represents a logic element in a circuit. The classes Signal and Gate are derived from LogicElement. A Signal represents a true or false input signal. A Gate represents an AND, OR, or NOT gate.

From your 'other' course, you know that the NAND gate is sometimes referred to as the Universal gate since a circuit using one or more NAND gates can be constructed to simulate the output of the other gates. (see graphic).

Tasks.

  1. Add the body of the Nand() method in the Gate() class. Be aware that one of three signals are possible on each of the inputs.
  2. Develop the AndGate, OrGate and NotGate classes derived from Gate. The getOutput() methods should mimic the Emulated circuit designs to determine the results.
  3. Recall the discussion of Reverse Polish Notation (RPN) in class last week. Develop the RPN class as defined by the following UML diagram that can be used with the TestGates driver to produce the given output.
Questions 3. GRAPHIC. (Degree of Difficulty:1.05)

Julia Sets

You will recall that the Mandelbrot Set consists of the set of points, c, in the Argand (Complex) Plane, whose orbits under the iterative formula, z <- z2+c never reach a magnitude greater than 2.0, where z starts at 0+0i.

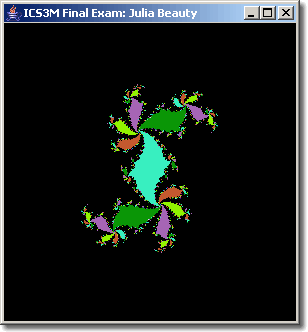
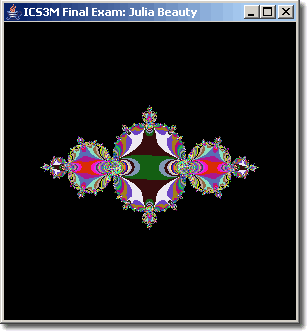
The algorithm for Julia Sets is very similar in that the orbits are also considered under the iterative formula, z <- z2+c, however c remains fixed over the entire map while -2.0 <= Re(z) <= 2.0 and -2.0 <= Im(z) <= 2.0. Two other important considerations are the number of ITERATIONS is carefully chosen and the magnitude is expanded to 10. Consider the examples below. The Black pixels are points that are not in the Set, the coloured pixels represent points that are in the Set in which the magnitude obtained is used to select a colour from the palette.

Task. Adapt the Platform Application used to generate Mandelbrot Sets to produce the following four Julia Sets. Feel free to use any palette you wish (even a random one as below).

Figure 1. c = 0.38-0.35i; ITERATIONS: 127 Figure 2. c = -0.123+0.745i; ITERATIONS: 127
Figure 3. c = -0.6672+0.459i; ITERATIONS: 31 Figure 4. c = -0.765+0.003i; ITERATIONS: 31