2004 ICS3MAP FINAL EXAM-Java
Friday, June 4th. 1:00 p.m.
INSTRUCTIONS TO STUDENTS.
- Students will complete ONE question from the following THREE alternatives.
- Superior scores will be reserved for solutions that reflect accuracy, clarity, design, and documentation elements.
- It is imperative that you name your files exactly as requested. Attach all (and only) the requested files to your email to handin at the end of the exam.
- You are allowed to use your textbook and Z: drive.
- You are NOT allowed to access the internet at any time during the exam.
- Good luck.
Area
 Preamble.
Next year, in your Calculus course, you will discover the importance
of determining
a value for the area between a function and the x-axis between
some left and right
boundaries.
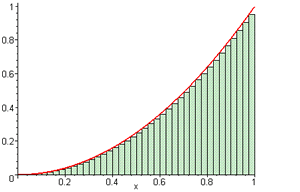
The graphic at the right, depicts an approximation to the area beneath
the function f(x)=x2 and the x-axis over the
interval from 0 to 1. The approximation is determined by carving the
interval from
0 to 1 into, say n pieces, and then using that measure as the
width of one of a series of rectangles whose height can be determined
by evaluating
the function at each x-value along the way. The approximation gets better
and better, the larger n is. Using this strategy, the area approaches
a value of 1/3 square units. The graphic below depicts an animated attempt
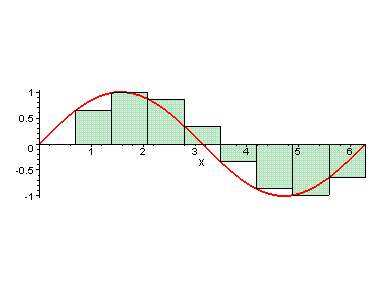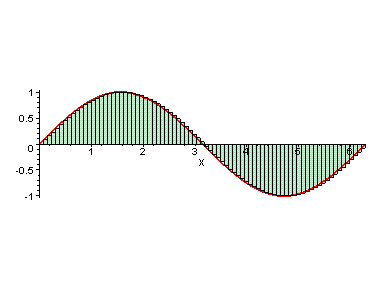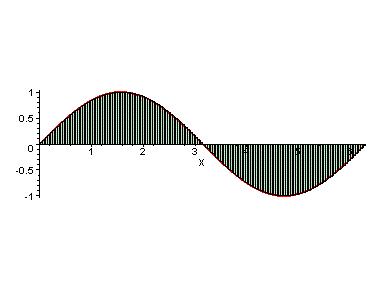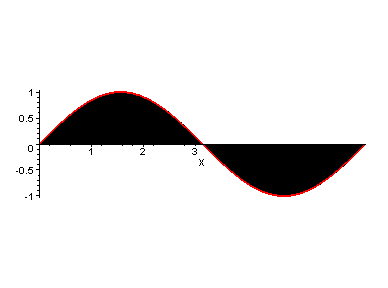
to determine the area between the function g(x)=sin x,
and the x-axis
over the interval from 0 to 2pi. Using this strategy, the area approaches
4 square units.
Preamble.
Next year, in your Calculus course, you will discover the importance
of determining
a value for the area between a function and the x-axis between
some left and right
boundaries.
The graphic at the right, depicts an approximation to the area beneath
the function f(x)=x2 and the x-axis over the
interval from 0 to 1. The approximation is determined by carving the
interval from
0 to 1 into, say n pieces, and then using that measure as the
width of one of a series of rectangles whose height can be determined
by evaluating
the function at each x-value along the way. The approximation gets better
and better, the larger n is. Using this strategy, the area approaches
a value of 1/3 square units. The graphic below depicts an animated attempt
to determine the area between the function g(x)=sin x,
and the x-axis
over the interval from 0 to 2pi. Using this strategy, the area approaches
4 square units.
Task. Develop the Java application Area.java, that will determine the area between a function and the x-axis, over a user-chosen interval and n value, using this rectangle strategy. Your program should offer the two examples depicted here and a third function of your choosing.
Geometry
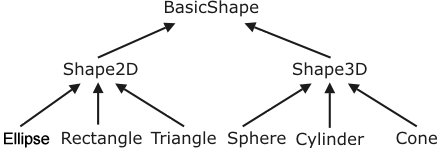
Preamble. Page 126 of your Student Agenda identifies numerous Shape objects and their quantitative formulas. This information could be organized into a crude taxonomy similar to the following,
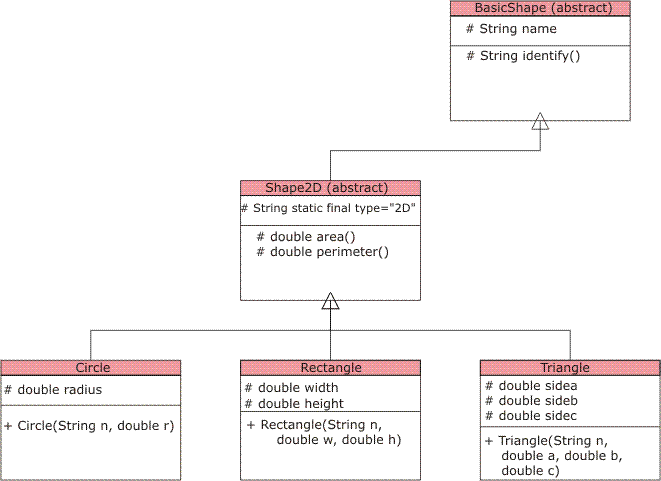
From the work we did this year, particularly the Marine Biology Case Study, you are familiar with the Object-Oriented Programming principles of Inheritance, Encapsulation and Polymorphism. For example, objects of the Circle, Rectangle and Triangle subclasses, would inherit all the functionality of their Shape2D superclass. In turn, since Shape2D subclasses BasicShape, the three concrete shape classes inherit BasicShape's assets as well. A similar inheritance line is true for the three dimensional side of the taxonomy. Through strategic class design decisions, maximum capabilities can be applied throughout the class structures. The Unified Modeling Language (UML) diagram below suggests how we can distribute our methods throughout the Shape2D branch of the taxonomy,
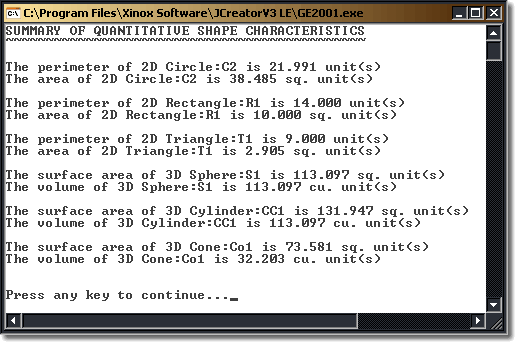
Task. You are to develop a Java application using the driver, Geometry.java, that will implement the class designs outlined above to produce the precise output below. Name your classes exactly as suggested. The only permissible changes to the driver will be between lines 35-37 and 41-43. (For the Triangle class, use Heron's Formula described on the board to find the area)
LSystems
Preamble. A straightforward algorithm for fractal generation, known as an L-System, named after Astrid Lindenmayer who originally conceived the idea in 1968, uses a pen (or what we will call a turtle), dragged across the canvas according to a set of instructions. The instructions are encoded as a String, where each character is interpreted as follows,
F |
Draw a line of length, D, in the current turtle heading |
+ |
Adjust the turtle heading right by an angle, d. |
- |
Adjust the turtle heading left by an angle, d. |
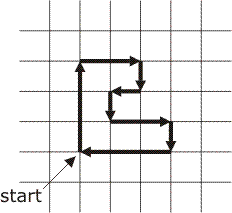 For
example, the String, FFF+FF+F+F-F-FF+F+FFF commands the
turtle to undertake the image to the right.
For
example, the String, FFF+FF+F+F-F-FF+F+FFF commands the
turtle to undertake the image to the right.
The fractal nature of this image creation process lies in the modification of the original string (the axiom) over successive generations. Consider the sequence of four images below. The first image is that of square that can be encoded as the String, F+F+F+F (n=0). If we substitute the String F+F-F-FF+F+F-F (the production) for every F in the axiom and then render the resultant string, we get the next generation (n=1). Subsequent generations (where each F is replaced by the production) can be undertaken and result in the images below (n=2 and n=3). In this example, D was initially set to 256 and reduced by a factor of 4 for each successive generation. The value of d, was 90°, and remained as such throughout the entire process.
Task. Develop the Java application, LSystems.java using a driver similar in structure to the platform used to develop your Mandelbrot application, to render the L-System sequence below. Finally, render the fourth generation (n=4) of a second fractal image defined by the axiom, +F, and a production of F-F+F+F-F. The image appears below.
n=0 |
n=1 |
n=2 |
n=3 |




