2009/2010 ICS4U Tasks
Trigonometric Lookup Applet. As our text mentions, certain results cannot be calculated on-the-fly due to unacceptable performance delays. Games often require fast mathematical results such as the value of trigonometric functions which can be relatively time-consuming to calculate if evaluated by standard means. In this assignment you are asked to generate the values of the six trigonometric functions for degree measures on the closed interval [0, 359]. The source of these values is a small lookup table of precomputed sin ratios for angles with degree measures over the interval [0, 45]. Through the use of arithmetic operations only (+, -, ×, ÷, and %) and simple trigonometric identities, you are to produce the results. Take a few moments to explore the adjacent applet.

Task. Create a project called LookUpApplet and either drop in this driver or create your own by the same name that fits with the only call you're permitted to make. Add the static class Trig.java to your project that contains the lookup table and the header for the getTable(int w) method. You are to complete the body of the getTable(int w) method and add additional methods that will result in a mirror of the adjacent applet. Your primary emphasis is efficiency. Avoid any unnecessary or redundant calculations. To accomplish this you will have to think deeply about trigonometric concepts and weigh the cost of each arithmetic operation (+, -, *, /,%) and decision (if, switch, etc). You are not allowed to use the Math class, nor any other class with mathematical methods or operations. Since you are developing an applet, you should always consider the characters available in the Unicode pages, particularly Box Drawing and Mathematical Operators for this assignment.

By the deadline, please submit Trig.java to handin and mount your applet.
BST Merge.If you think clearly and deeply before hitting the keyboard, you'll produce a superior result and make the deadline with plenty of time to spare. Translation? Grab a piece of paper and a pencil.

Task. Create a new BST object by merging two existing ones. Review this documentation and the read pp. 586-589 where the author discusses a Do-It-Yourself BST. In particular, look at the add method on Page 588.

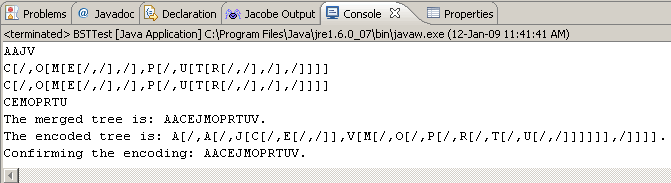
Adding the following lines to your BSTTest.java driver, 

    // Merge and Confirm
    BST bst3 = bst.merge(bst2);
    
    System.out.printf("The merged tree is: %s.\n", bst3);
    System.out.printf("The encoded tree is: %s.\n", bst3.getCode());
 
    //Confirm encoding
    BST bst4 = new BST(bst3.getCode());
    System.out.printf("Confirming the encoding: %s.\n",bst4);

results in the following output,

BST Construction from an Encoded String. Supply an additional BST constructor with the following signature, 

  /**
   * Constructs a BST object from the parameter containing the  
   * encoded Binary Search Tree.
   * @param code the encoded binary search tree
   */
  public BST(String code) {
    this.code = code;
    root = parse();
  }

This constructor calls the iterative method parse(),

private TreeNode parse() {
	Stack<TreeNode> stk = new Stack<TreeNode>();

}

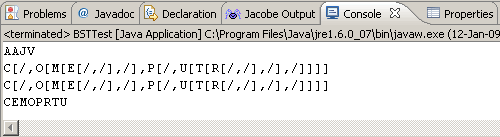
that uses a local java.util.Stack<TreeNode> object to assist with the construction of the BST. Adding the following statements to your current driver,

    // From an Encoded String
    String code = "C[/,O[M[E[/,/],/],P[/,U[T[R[/,/],/],/]]]]";
    System.out.println(code);
    BST bst2 = new BST(code);
    System.out.println(bst2.getCode());
    System.out.println(bst2);

will yield the following output.

Manual Creation and Traversal. In this first assignment, you are to incorporate TreeNode.java, exactly as it appears on page 581 (get student files from Skylight), into the development of a BST class whose source code prototype appears below. The BST constructor will use one statement to construct a tree with four nodes. Complete the body of the traverse(TreeNode node) method and use the driver file, BSTTest.java to test that the characters appear on the console in alphabetic order. 

public class BST {
  
  private TreeNode root;
  
  /**
   * Constructs a BST object encapsulating a binary search tree 
   * into 'root'. Hard codes the Character data: 'J', 'A', 'V', 'A'
   * as the node values in one statement (manually).
   */
  public BST() {
  }
  
  public void traverse() {
    traverse(root);
  }
  
  private void traverse(TreeNode node) {
    if (node != null) {
	  // add code here so that all names are displayed to the console
    }
  }
}

Explorer. The file organization on your laptop's hard drive is a suitable example of a composite list of the type profiled on pp. 551-554 of the textbook. Each entry is either a file or another folder. In this assignment, you are asked to develop your version of Explorer.jar that can be used to display the file/folder contents of the entered path in a manner that incorporates indentation to reflect the hierarchical organization of the file structure.

Task. Develop the class Explorer as a simple, efficient extension of JFrame that can be used to display the contents of a folder. The TextArea object is to be populated by a String returned from a recursive method that explores the path to the folder supplied by the user in the TextField. The only Swing components you are permitted to use are JFrame, JLabel, JTextField, JTextArea and JScrollBar. Note. You'll find the File class handy for distinguishing between a file and a folder (directory).

You'll find plenty of examples that incorporate Swing components here.

Rollover...The Collage Theorem. With the concepts of Iterated Functions Systems and Cramer's Rule under your command, you are now able to undertake the extraordinary step of being able to model and render a great number of natural and manmade images on your own.

The IFS codes provided in the Iterated Function Systems project provided the 'seed' with which to 'grow' the attractor through iteration. The codes defined the matrix elements of a finite set of affine transformations coupled with the probabilities associated with their chances of being applied. The Collage Theorem describes how the process can be reversed.

Starting with the final desired image (attractor), you can tile the image with similar contractive images (a photocopier is helpful with this). Rollover the image to the right to see an example. Mapping where points on the final image end up, provides you with a system of equations in which the variables are the elements of the matrix definition of the affine transformations. This system of equations can be readily solved with your Cramer's Rule project.

Task. Render the image you have been assigned on our course page. Using a process similar to the one we undertook last class, discover the IFS codes for your image, add it (them) to the IFS menu of your LSystems project, and remount the applet on your home page, accompanied by an explanation on your web page. Submit all source code by the deadline.

Cramer's Rule. One method for solving a relatively simple system of n equations with as many unknowns acknowledges Gabriel Cramer (1704-1752) for a computationally-friendly algorithm. Here's a description,

  1. Consider a system represented in the matrix form, Ax=b, where A is the n×n coefficient matrix, x is the variable column vector with n elements and b is the right-side column vector with n elements.
  2. Let Ac be the matrix obtained by replacing column c with b.
  3. Let the determinant of A be represented as D.
  4. Let the determinant of Acbe represented as Dc
  5. Cramer's Rule defines the solution to the system as,


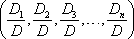
    where D is not zero.

Task. A little over a year ago you were asked to create a static NumericalMethods class in support of the Newton's Method Root Finding project. Dust off that class and add new methods in support of the following. Create a project entitled Cramer and drop in this driver. Do not modify the driver with the exception of defining new values for A and b. Add the required methods to your static NumericalMethods class supported by well thought out and efficient supporting methods to allow the driver to obtain the correct result for any n×n linear system using Cramer's Rule. Submit your javadoced NumericalMethods class only by the deadline.

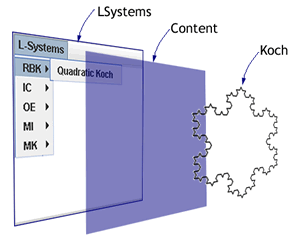
Iterated Function Systems (IFS). In this assignment you are asked to add a fourth column to your LSystems applet entitled IFS, that will permit the user to view a rendering of each of the IFS in the table below. One design suggestion would be to create a Code class to encapsulate the various affine transformations, their probabilities and the colour palette. All IFS images could be stored in a TreeMap<String,Code> where String is the name of the IFS, thereby making retrieval relatively efficient. This structure could be initialized within the constructor of the Content class.
IFS
Fern #2 (lower)

MODELING IN R2: PART 3. Animation2D . In this final instalment, we integrate the foundation classes you have developed over the last projects to demonstrate the applicability of matrix-defined transformations to simple, but compelling, two-dimensional animations. Ireland Comery's effort appears to the right.

Task. Create the project, Animation2D, and add this driver. Configure your build path to include your Transform2D classes to access Transform2D, Matrix2D, Point2DList, and Point2D. This is the best of both worlds, since we're only keeping 'one set of books', so to speak. Look over the driver code. The general idea is to transform a Sprite object(s) to the coordinates for the next frame within the updateScene() method. The loop in the run() method will then call the paintPanel() method in which you can retrieve your Sprite's updated coordinates to populate a Polygon object. This polygon object can be added to the scene through a call to Graphic2D's draw() method. Here's the full Javadoc. I've created a very elementary example to the right. Considering your vast exposure to gaming animation, I know you'll take your effort to a whole new level.

Note. The classes in this project reflect a strong hierarchical design. I would expect your code to capitalize on the strength of this design; writing tight, efficient carefully-crafted statements that fully exploit the cascading nature of the respective class methods.

Submission. Attach only your Animation2D and Sprite classes and a video of your animation (you could use CamStudio) to an email to handin with the Subject: Animation2D by the deadline. I will use your supporting classes submitted earlier. Here are some samples from previous years:

MODELING IN R2: PART 2. Transform2D. In this second instalment, you are asked to create a project called Transform2DTest, using the driver, Transform2DTest.java. Add the class file Point2DList.java and implement the supporting Point2D. Configure your Transform2D project to refer to your Matrix2D class found within your Matrix2DTest Project, as I will when I evaluate your work. Note that this is a far safer project design as you are not maintaining two or more versions of the class.

Task. Write the two class files, Transform2D.java and Point2D.java, that will work seamlessly with the other existing classes to produce this output. I have prepared the documentation that will guide your effort.

Please attach the following separate class files: Transform2D and Point2D, to an email to handin with the Subject: Transform2D by the deadline.

MODELING IN R2: PART 1. Matrix2D. Develop a set of (integrated) constructors for the class, Matrix2D that can be used with the driver Matrix2DTest.java to produce this output.
Note 1. Make every attempt to maximize the use of a minimal set of methods.
Note 2. Minimize the dependency of your code on direct references to the only instance field, matrix.

Javascript Collection Framework: Josephus Ring. 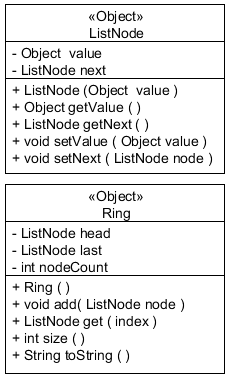(I'm really excited about this assignment because the five of you are the only students that could write it)
Once upon a time, back in BTT1O, you wrote some amazing code in Javascript. Check out what you did. Three years later you find yourself immersed in the Java Collections Framework examining a set of ready-made collections for modeling data. Since you'll likely be coding at various times in your life for either pleasure or profit, you may find yourself in an environment that doesn't offer such richness.
ICS3M introduced you to the Josephus Flavius Game. Closing a singly linked list into a circular list (ring) is a perfect model for this activity both visually and conceptually.

Task. (Few activities speak to the mastery of a programming concept more than one which involves its translation from one language to another) Although we haven't got time to translate the entire JCF (you have to go to university soon), we can build an elementary prototype of one of them. Examine the Javascript of this page to refresh yourself on some basic Javascript syntax. You will also find W3Schools and this Object tutorial useful. You are asked to write a Javascript Ring class enhancement of Java's LinkedList class that will serve as the data model for your successful implementation of the Josephus simulation. Implement the basic UMLs to the right in the same file as Josephus.html and add additional functions (methods) as required paralleling as closely as possible those in Java's LinkedList Class. When completed, place the two object definitions in a separate Ring.js file and link to it from Josephus.html. In this way your Objects can more easily be integrated into future scripts. Submit both Josephus.html and Ring.js files by the deadline. I'll mount successful implementations from our home page for vistors to admire.

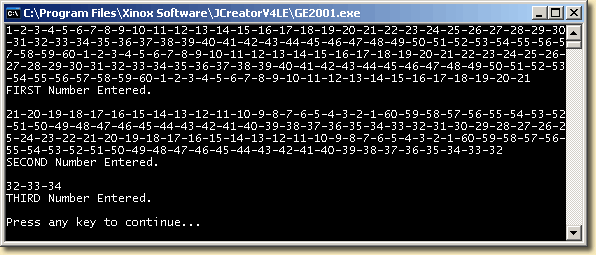
Combination Lock. Since Java's LinkedList<E> class maintains this data structure as a doubly-linked list, users can traverse it forward and backward with the help of a ListIterator object. Using the driver, LockTest.java, develop the class file Lock.java, defined by the UML specification below.

With a correct implementation of the Lock class initialized with the combination, 21-32-34, your driver will generate the following output,

Network. It has been decided that students are spending too much time studying and not enough time socializing. To address this situation, it has been decided to give every student a friend. Friendship is one-way. That is, if Robbie is assigned to be Mark's friend, Robbie must be friendly to Mark, but Mark is not required to reciprocate. The assignment of friends is done by computer using student numbers. Every student is assigned exactly one friend. Sometimes, a ‘circle of friends’ occurs. For example, if Max is assigned Owen, Owen is assigned Ireland, Ireland is assigned Ernest, and Ernest assigned Max, we have a circle of 4 friends containing Max, Owen, Ireland, and Ernest. In the circle, we can say that Max has a separation of 0 from Owen, of 1 from Ireland, of 2 from Ernest, and of 3 from Max.

Task. Given the computer assignment of friends, determine whether two students are in the same circle of friends, and if so, determine their separation.

Input Specification. Input begins with a single integer n (2 ≤ n ≤ 9999), on a line by itself, indicating the number of students in the class. The next n lines contain the computer assignment of friendship. An assignment is of the form x y (where 1 < x < 9999, 1 < y < 9999, x ≠ y). For example, 1234 8765 is a possible friendship assignment indicating that student 1234 must be friends with student 8765. Following the friendship assignments, there are a series of lines containing two student numbers, separated by a single whitespace. These lines represent the pairs of students that you will determine if they are in same circle of friends and, if so, their separation. The last line of input can be identified by the use of the 0 0 as the friend assignment.

Output Specification. For each case, you are to print, on a separate line, either Yes or No depending on whether they are in the same circle of friends. If the answer is Yes, follow the output Yes with a single whitespace and then an integer indicating the friend’s separation.

Sample Input:

6
1 2
2 3
3 1
10 11
100 10
11 100
1 100
2 3
0 0

Output for Sample Input:

No
Yes 0

Java Collections Framework: Queues. H1N1 Clinic Simulation. (There are specialized languages for running simulations. We can employ Java to get a feel for the value of this kind of exercise.) As an expert in the field of Operations Research, you have been contacted by Ontario's Ministry of Health to provide advice on the timing of opening up the vaccination program to the general public, now that high priority groups have almost all had their shots. The danger is that if they open up to the genral public too soon, longer lineups from increased demand will overwhelm their resources.

A queue is a FIFO structure. From the data given to you, citizens (instances of the Citizen Class) arrive in random intervals of 1 to 4 minutes. Also, each citizen is vaccinated in random integer intervals of 1 to 4 minutes. Obviously, the rates need to be balanced for line lengths to remain manageable. If the average arrival time is larger than the average vaccination service time, the queue will simply continue to grow. Even with balanced rates, randomness can still cause frustratingly long lines.

Task. Run a simulation for a 12-hour day (720 minutes). For each minute of the day:

Output should look similar to the following,

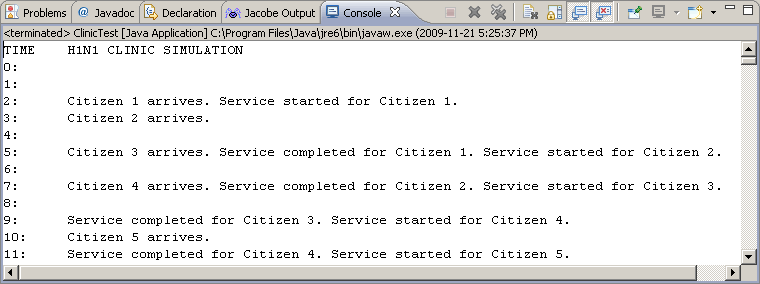
aintain the necessary data so that at the end of the simulation, the program summarizes and displays results for the following:

Run the simulation 10 times and use the data to complete this Excel workbook. Now, the OMH has a conern that if the clinic opens too soon, before are the special groups (pregnant women, children and seniors), demand will be result in arrival times reducing to between 1 and 3 minutes. Perform 10 more simulation runs with this reduced arrival time and record your results in the workbook, alongside the original arrival times of between 1 to 4 minutes.

Final Recommendations,

Using the driver ClinicTest.java develop and submit the Clinic.java and Citizen.java class files that will yield output similar to the above along with a completed Clinic.xls file with your recommendation for whether the clinic should be opened to the general public now or wait until the special needs groups have been vaccinated.

Sorting Applet. You've had some experience with sorting algorithms (Selection Sort, Insertion Sort, MergeSort and QuickSort) . In this final assignment of the term, you are asked to combine this knowledge with your familiarty with applets to develop a graphic interpretation of one or more of the algorithms. Numerous online sorting applets exist that you are encouraged to consult for design inspiration. on the other hand the code you submit is expected to be entirely yours.

Create the project Sorts and mount the resulting applet on a web page supported by an explanation of each of the algorithms you have implemented.

Plane-Filling Curves. Part 3 of 4: Bracketed L-Systems. The experience you have gained in the generation of Koch and FASS curves can now be extended to the rendering of plant-like images. The original idea is credited to Astrid Lindenmayer, who, in 1968, proposed, "an axiomatic theory of development" for plant structure. Hence the name L-Systems. Although we're sticking to the 2D version for the time being, here's a 3D example.

You are asked to supply the code necessary to reproduce the images described on page 25 of the Algorithmic Beauty of Plants. To facilitate the branching characters inherent in plants, the productions introduce brackets. Your rendering method will interpret the open bracket '[' as a command to preserve the current drawing state (position, heading, and possibily color and line thickness), to be restored on the encounter with the next close bracket ']'. In this way, your drawing algorithm can 'return' to a node and continue drawing in another direction.

 

To facilitate the saving and restoring of the drawing details you will create an inner Turtle class of the Content class as suggested by the adjacent minimal UML diagram. This will require a few modifications to Koch's draw(Graphics g) method in which the drawing details are encapsulated with an active Turtle object. A local Stack<Turtle> within draw(Graphics g) can assist with the saving and restoring of the drawing details. Here are a couple of L-System 'Gardens' authored by the 2008-2009 ACES, and the 2007-2008 ACES.

Task. Implement the project as defined above, incorporting all 6 of the L-Systems defined on page 25. Update your Applet and ensure that curves from Parts 1 and 2 remain fully functional under these enhancements.

If sufficiently inspired, add colour and/or line thickness properties to your Turtle class as previous years have done. Also, research other Bracketed L-Systems and add additional menu items for the rest of us to enjoy.

FASS
ACES
Dragon (1.10a) IC2
Sierpinski (1.10b) RBK2
Gosper (1.11a) MI2
Peano (2.7a) MK2
Hilbert ( 2.7b) OE2
Plane-Filling Curves. Part 2 of 4: FASS Curves. Here's a quote from page 12 of the Algorthmic Beauty of Plants,

 

The curves included in Figure 1.11 belong to the class of FASS construction curves (an acronym for space-Filling, self-Avoiding, Simple and self-Similar) [116], which can be thought of as finite, self-avoiding approximations of curves that pass through all points of a square (space-filling curves [106]).

 

For our purposes, what separates these curves from the Koch class of curves of Part 1 are the presence of multiple keys and corresponding productions in the definitions. This has an immediate implication for our recursive generation method in that String's replaceAll method is not designed for the simultaneous replacement of multiple Strings.

Task.
  1. Modify the generate() method of the Koch class to accommodate multiple keys and productions
  2. Provide an implementation of the FASS curve (Islands) defined in Figure 1.8 on page 9.
  3. Provide an implementation of your assigned curve shown in the table above.
  4. Upgrade the applet on your web site posted in Part 1 to include these two curves, accompanied by the details of both curves (name, number of generations, angle, axiom, productions, etc.)

Plane-Filling Curves. Part 1 of 4: Koch Systems. As a starting point, read Exercise P13.15 on page 623 of Horstmann. Create a project called ExP18_15, download the files from here (Chapter 18, Problem 15) and execute the project. The Koch Snowflake is an iconic example of a class of fractals known as plane-filling curves or PFCs (originally they were known as topological monsters due to their curious mathematical properties).

The realization of this group assignment will be a common applet that will reside on each of your home pages as well as our ACES main page. Each of you are asked to develop a different member of the family of PFC's as indicated in the table below (given sufficient interest, investigation of space-filling curves (SFCs) could be undertaken later in the course). Using a recursive generation strategy to propagate the L-System definition, your Koch object will then render the final curve using the graphics reference passed to it from the Content object. Your assignment will be to develop your Koch class and Koch.html that includes the L-System definition of your PFC together with details of it's fractal dimension. These explanations will be added to the common web page carrying the applet. Submit a replacement for the java statement containing the constructor call to your Koch object that is to be inserted into the actionPerformed() method, Koch.java and Koch.html to handin by the deadline.

Rather than supply you with a UML definition for Content's nested Koch class, review the javadoc here. Note that although the twelve instance fields of the Koch class appear in the public interface, they should all be declared private. Here is the source code that contains definitions for the LSystems, Content and the stub of Koch. (Note. Ireland Comery's Parametric Equations assignment was used as a base for this project since it reflected excellent class design)

Extra. For the motivated, a useful technique for the future is to prepare an animated gif from the saved renderings of each stage in the development of your PFC. An example appears below and this is the same technique I used in the creation of the ACES logo in the top right corner of our home page. Alternatively, who's up for the origami version?

References are to the Algorthmic Beauty of Plants (pp. 9-10):

ACES
Koch System
RBK
Figure 1.7 a)
IC
Figure 1.9 a)
OE
Figure 1.9 b)
MI
Figure 1.9 c)
MK
Figure 1.9 f)

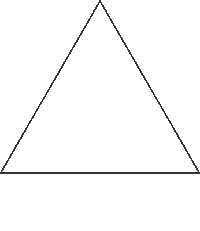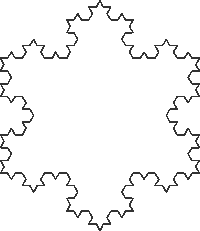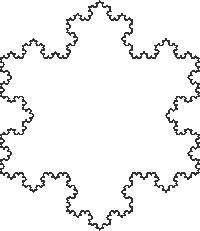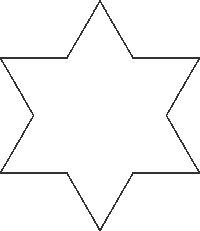Task. Implement the body of the LSystems.Content.Koch class so that it displays your assigned Koch curve when users select your curve and the Triadic Koch Snowflake when he selects all other Koch menu items. If you're inspired, feel free to complete some or all of the others Koch systems as well. Mount the applet on a web page within your site that includes, at the very least, the definition of your Koch curve (axiom, production, delta, etc.) together with a presentation of the determinaton of the fractal dimension of your PFC.

Pascal's Triangle and the Binomial Theorem. This assignment comes in three parts, all three of which are to be submitted to handin but only the third of which is to be mounted on your site as an applet.

Part 1. PascalRecursive. Display the first 30 rows of a left-justified Pascal's Triangle in which the terms are determined recursively. Set the Font characteristics of the display such that the text appears in columns.

Part 2. PascalIterative. Display the first 30 rows of a left-justified Pascal's Triangle in which the terms are determined iteratively with an emphasis placed on minimizing the amount of storage required for variables throughout. Set the Font characteristics of the display such that the text appears in columns.

Part 3. BinomialTheorem. You are to develop a web page that showcases Pascal's Triangle and the Binomial Theorem. The page will contain an applet that extends Part 2 (iterative strategy) to include as many rows as there are in the height of your panel (make it at least 500px by 500px). However, instead of displaying the actual numbers, you are to plot a pixel for only the odd terms (the resulting image should be suprisingly familiar).

Supporting content of your applet will include an image captured from your Part 2 project that displays the actual numbers and an explanation of the application of the triangle to the Binomial Theorem. I have prepared this Word document which you are free to capture an image from and use. Be sure to title your web page appropriately and mount the page on your web site. Submit the source code for the three Projects: PascalRecursive, PascalIterative, and BinomialTheorem by the deadline.

The Chaos Game. To further explore how structure can be coaxed out from seemingly random activity, you are asked to implement a relatively new algorithm known as the Chaos Game. Before starting the 'Game', mark any three fixed points on a piece of paper or Java panel (think of them as vertices of a triangle) and any fourth point, P. On each turn, you are to generate a random integer in the range from 0..2, and mark a new point, P', that is equidistant from P to the respective vertex. Continue this process, generating a vertex number and plotting a new point halfway towards the vertex.

After 1 000 000 turns the locus of points obtained will likely surprise you. Document your code and mount your jar file by the deadline.

Circle As a Limit. Develop and mount an animation as an executable jar in which the number of sides of a regular polygon increases until it appears to approximate a circle. The circumscribed limiting circle should appear in each frame for reference. Each frame in the animation should also include quantitative values for the radius, perimeter, and area of the n-gon.

 

 

 

 

 

Catalog of Parametrically-Defined Special Plane Curves. In this assignment you will investigate a number of interesting plane curves often left unexplored in high school. Indeed, some of these parametrically-defined curves are so compelling, strange names have been evolved to identify them. These include, Nephroid of Freeth, Bowditch, Rhodonea, Conchoid of Nicomedes, and Tschirnhausen's Cubic to name a few.

Task. Develop and mount the applet, Catalog, that will permit the user to select from a menu containing at least 6 interesting examples of special plane curves under the menu name, Parametric. Recall that by changing one of more constants within a given parametric definition, a visually impressive family of curves can be displayed.

In addition to developing the applet, you are asked to provide content on the web page to support your choices (names, history, equations, domain, etc). You could use Word's equation editor to create equations and then copy and paste them into a paint-like application (like Mac's Preview?) to obtain the graphic images. Include citation links on your web page. The image to the right appears at, http://steiner.math.nthu.edu.tw/disk3/gc-02/famous-curves/parametric.html.

Note. Due to the Thanksgiving holiday, you have two weeks for this assignment. I recommend starting your research early to allow you enough time for inspiration to work its way through to your work. There are numerous sites that allow you interactively explore the geometric foundations of the loci that some of you may find quite rewarding.

CBC Logo. Examine the CBC logo. Develop and mount the Java application CBC.jar that efficiently incorporates affine transformations of filled circles to generate the image.

 

 

 

 

 

 


Toyota Logo. For your first Java2D assignment you are asked to recreate the familiar logo to the right as closely as you can. Some of the areas you will need to investigate include,

Create a project called Toyota and adapt your Ultimate platform with the aim of developing an efficient, menuless application that you are asked to mount on your home page as an executable jar by the deadline.

Note. An important consideration is the scalability of your rendering. As can be seen from this example, as the frame is resized, the image remains proportional, centered horizontally and scaled to ensure it remains entirely within the panel.

Ultimate Platform. Consolidating what we've learned from Chapter 1 into a dual Java2D platform would be both instructive and useful as we go forward. Create a new project under the name Ultimate and incorporate the following features,

Finally, add Ultimate to your home page as both an executable jar and an applet to confirm. Submit your source code to handin.

Read Chapter 1 (pp. 1-27) and consider answers to the Review Questions on p. 29. Be prepared to contribute to a discussion on the material at the start of class.