RSGC ACES: The Calculus Project

12. Function.integrate(). As the inverse operation of the well-defined differentiation operation, one would think integration is just as clear cut. However, as you've discovered, if differentiation is a science, integration is an art. In recognition for how advanced your Calculus project is, I'm giving you a lot of latitude with this final segment. Here's what I suggest.

  1. Add the public boolean isIntegrable() predicate method to your Function class that clients can use to confirm whether your application can perform the operation.
  2. This method could first create a String representation of the structure of your yTree. You already have a reportStructure() method that could be used as design model for a more detailed encoding.
  3. This String can now be compared to an array (matrix or map) of patterns you feel you can create integral Expression Trees for.
  4. Pass the index (or encoded integral String) into the array determined in the previous step to the private ENode integrate(int i) method that will construct the integral.

Add methods to your driver to test your new features. Remember to add -1 to your 'f method (see Step 4) so that clients can evaluate the integral of your function.

11. Function.compose. Your Function class preserves the user's definition of f(x), but what about String representations of f'(x) and f"(x)? For these results we require a method that performs the inverse of your parse() method: returning an explicit String from an ETree. This is a challenging but highly rewarding method to write!

Develop the recursive method,

	private String compose (ENode root)

that should be invoked on dyTree and d2yTree to enable your Function class to present String representations of f'(x) and f"(x) to users.

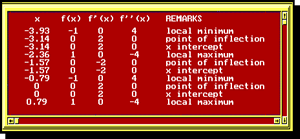
10. Function.analysis. (New for 2015). With the roots of the system of functions available, a reasonable analysis of a function can be undertaken. This task can be broken down into two sections, the analysis of discrete behaviour (`x`-intercepts, extrema, points of inflection) and the analysis of interval behaviour (positive and negative range, increase and decrease, and concavity).

Required Task (Discrete)

For each of the functions in RootHarness.txt you are to present an analysis of the `x`-intercepts, extrema, and points of inflection. Using the driver Calculus.java (slightly enhanced from the previous stage) will produce this output.

Elective Task (Interval)

As an elective task that can be used as a replacement for an earlier Calculus stage, have your analysis include interval behaviour for positive and negative range, increase and decrease, and concavity.

9. Function.roots. The key to the analysis of functions is the ability to determine the roots of the functions within the system that includes, `f(x), f'(x), and f''(x)`. Two standard Numerical Methods for Root Finding are known by the names,

Task.

  1. Consider employing the new resources highlighted in the adjacent UML diagram in your application of the Bisection and/or Newton-Raphson root-finding Methods.
  2. As a benchmark, use this RootHarness.txt file to obtain this output.

Considerations.

  1. You might find the method Math.signum(double d) handy in the application of the Bisection Method.
  2. To obtain the roots of the `f''(x)`, you will need to determine `f'''(x)`.
  3. Tailoring the roots for presentation is challenging. For example, a numerical method may leave a root of 1.0 as 0.999999875. It needs to be trimmed up.
  4. We'll avoid discontinuous and non-differentiable functions for this purpose.
  5. Although we'll be setting the Calculus Project aside for this year after the Analysis segment after the Break, you very well may be inspired to enhance the terrific tool you've developed by the topics the lie ahead in your Calculus class. If you are, propose it to me as a Elective, we'll discuss the treatment of the topic, and off you'll go! The world you're heading into is drawn to inspired individuals. Be one.

8. Function.prune. You'll notice in the differentiate segment below that statements involving calls to prune and compose methods were commented out. It's now time to implement these methods.

A side effect of the differentiation activity results in subtrees that must be simplified. Typical patterns include,

`0+?, 1*?, ?^1, ?^0 (?\ne 0)`, COC, and FC

to name a few. In situations like these, expression trees require 'pruning'. Develop the recursive method,

	private ENode prune (ENode root)

that should be invoked on dyTree and d2yTree at the correct moment (ie. differentiating an ETree prior to pruning incurs future performance and efficiency penalties).

7. Function.ErrorCode. Division by zero, a negative radicand and a domain error are situations that can bring your evaluate() method to a dead stop. In this final segment you are to add defensive code to warn of such occurrences, everywhere you can think of.

Exception-handling would be the preferred technique (if you have the courage- go for it) but a lighter approach would simply be to anticipate a possible illegal evaluation beforehand and set the value of a global variable appropriately, prior to returning a value of, say, 1.0. Your own code and that of clients would be responsible for accessing your Function class's public int getErrorCode() method to determine whether the result of the evaluation is to be trusted. An error code of 0 means a successful evaluation. Other codes can be assigned as you deem appropriate. Don't forget to reset the ErrorCode to 0 prior to any evaluation.

6. Function.differentiate(). This is arguably the most satisfying stage of the project as it doesn't take too much coding to open the window to many applications. As you are well aware, there are five derivative 'rules' (Power, Sum, Product, Quotient and Chain). The first four are triggered on the occurrence of ONodes in your Expression Tree, and deserve methods in their name. Since the Chain Rule is simply the recursive application of the other four derivative rules, its application in our context, is transparent.

Task. Add the methods suggested by the UML diagram. With the exception of the last method, there should be self-explanatory. In the case of the recursive duplicate() method, deep copies of Expression Trees are required in a number of derivative contexts and I've found that it's quite handy to call on a single method to deliver the copy of the ETree. Once developed, temporarily add the following code to your Function's constructor to test the strength of your methods.

	dyTree = differentiate(yTree);
	//dyTree = prune(dyTree);
	System.out.println("dyTree Structure: " + reportStructure(1));
	//yp = compose(dyTree);

	d2yTree = differentiate(dyTree);
	//d2yTree = prune(d2yTree);
	System.out.println("d2yTree Structure: " + reportStructure(2));
	//ydp = compose(d2yTree);

5. Function.parse(). All the necessary infrastructure is in place (expression grammar, preProcess(), ENode hierarchy, reportStructure() and evaluate()) for software to assume the responsibility of creating the Expression Tree from a function defined as a String.

Add the following statement to your Function constructor,

	yTree = parse()

and a sequence of mutually recursive methods starting with, 

	private ENode expression()

that are used to support and enforce the grammar you created at the beginning of this Project. This interdependent suite of methods forms what is referred to as a Recursive Descent Parser. The RDP manipulates a class variable (int c for cursor, works) that acts as an index into the preprocessed string definition of the function. I would recommend the use of a healthy suite of predicate helper methods (to make your code read well) either built-in or developed by you. For example, the Character class offer isDigit(char ch) and isLetter(char ch) to name a couple of methods.

After the parsing is complete, an Expression Tree has been assembled corresponding to your function. Be sure to have your driver call reportStructure() to confirm the expected tree structure, followed by a call to f(0,x) to lock in your delight :)

4. Function.evaluate(). Add the following statement at the end of your Calculus driver, 
  System.out.printf("f(%3.1f) = %3.1f\n",1.5,f.f(0,1.5));

The intent of the call is to obtain the value of `f(1.5)`. If the Function f is defined as `f(x)=2x+1`, and your code is functioning properly, the output should be f(1.5) = 4.0. To support the call, add the following methods to your Function class.

	public double f(int which, double x)
and, 
	private double evaluate(ENode node)

For the f method, the value of the parameter which is 0 for `y`, 1 for `dy/dx` and 2 for `{d^2y}/{dx^2}`. The f method sets the value of the class variable x and then calls the recursive evaluate method to determine corresponding range element, passing it a reference to the root of the requested function's expression tree.

To test your code's ability to evaluate FNode's correctly as well, comment out the manual assembly of the Expression Tree for `f(x)=2x + 1` and replace it with the function `f(x)=log(100sin(x))` and test it with the driver call,

	System.out.printf("f(%3.1f) = %3.1f\n",Math.PI/2,f.f(0,Math.PI/2));

If your code is functioning correctly, the console should display a value close to `2.0`.

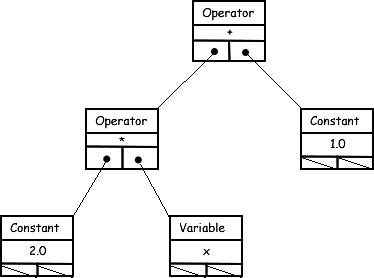
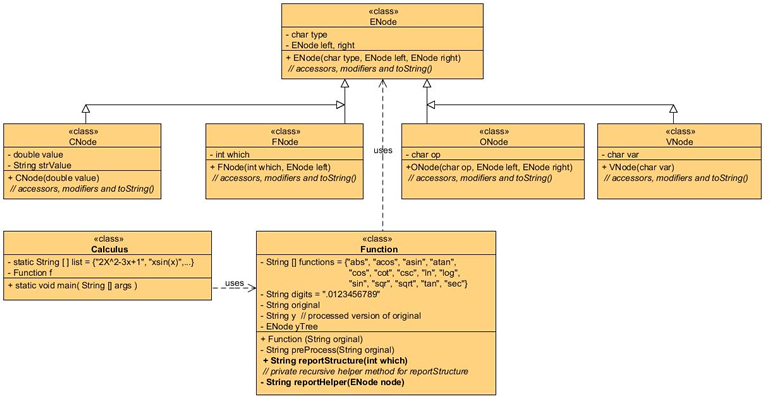
3. Function.ENode. The role of the parser (which we have yet to write) will be to construct an Expression Tree (yTree). Just as our earlier studies incorporated classes such as ListNode and TreeNode, we need to develop and implement an ENode class hierarchy whose objects can be used as the fundamental building blocks of our yTree. For example, consider the resultant yTree at the right generated from parsing the expression, 2x+1. This simple example suggests ENode subclasses such as ONode, CNode, and VNode. Throw in an FNode subclass and we should have everything we need for secondary school functions.

Task.

  1. Add this new driver to your Calculus project.
  2. Implement the classes in the ENode hierarchy defined by the UML diagram below within your Calculus project.
  3. Within the Function constructor, manually construct an Expression Tree for the y = 2x+1 in a single statement, referencing the root using the class field, yTree.
  4. To your Function class, add the method,
     public String reportStructure(int which)
    that, with the support of a recursive helper method, returns a coded String identifying the infix structure of the Expression Tree. This example should return: COVOC

2. Function.preProcess(). Create a project called Calculus and drop in this driver. Add a class called Function whose constructor receives a String definition of a mathematical expression. Add public String toString() and private String preProcess() methods to your Function class. The latter method modifies the expression in manner that makes it more compatible for the later stages of your analysis. Before you begin it would be wise to refresh your memory of the methods offered by the String Class. Alternatively, the underlying array structure of the StringBuffer class and the methods it offers might be justified. Methods you might find particularly useful include charAt(), indexOf(), and insert().

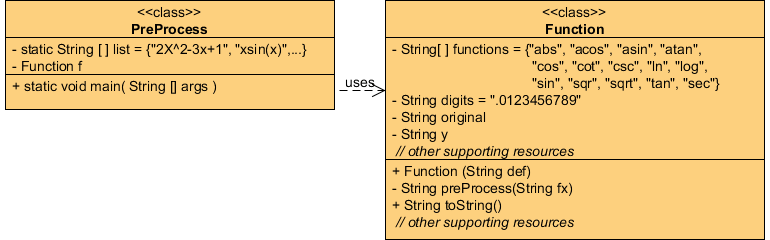
Considerations should include,

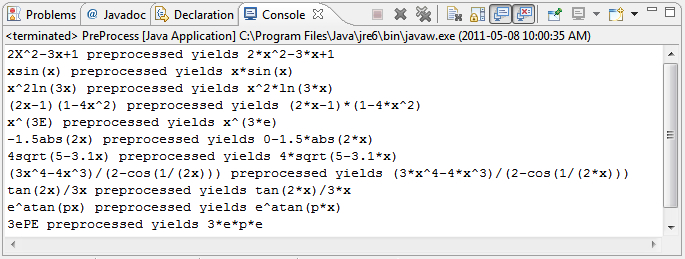
NOTE: From the outset you are encouraged to heavily document your work. It's amazing how quickly you will forget why you coded the way you did. The output should appear as follows (e stands for e, and p stands for π),

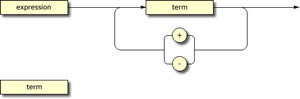
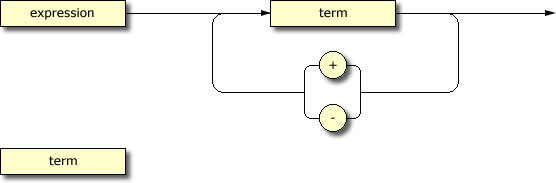
1. Syntax Diagrams for Expression Grammar. Of all the assignments you've been asked to complete over the past couple of years, you'll likely remember this as one of the most satisfying. As could be expected of a comprehensive project, it attempts to tie together some of the most important concepts within the co-disciplines of mathematics and computer science. For years to come, you will marvel at what you are about to accomplish. Finally, since your exam will expect that you extend this work in some new direction, you are encouraged to develop efficient and well-documented code.

The first step in writing IMAGE-Algebra&Geometry many years ago was a three-month investment in developing a grammar for the language before an interpreter could be undertken. Similarly your first step in developing application software to manipulate mathematical expressions is to develop an unambiguous grammar for the expressions you hope to interpret.

Using appropriate knowledge and vocabulary, complete a sequence of syntax diagrams for the broadest range of mathematical expressions you have encountered to this point in your development. Here's how the set of rules will start out. You should consider including most (if not all!) of these definitions in your grammar.