For the Binary Search Algorithm to be effective the data must be ordered. Although we capitalized on the static java.util.Arrays class to do the sorting for us last week, it is necessary to investigate the various algorithms in more depth.

The search for a fast, efficient sorting utility has led to the development of numerous algorithms over the last half-century. Some strategies are easy to understand and code, but can execute relatively slowly. Others are extremely fast, but challenging to understand and maintain. In these exercises, we will explore the details of four important algorithms (Selection, Insertion, Merge and Quicksort).

Once you have a feel for the mechanics of the Selection Sort, complete the following tasks,

1. Create a project called SortingAlgorithms and drop in this driver.
2. Implement the statements required by the comments within the code. Start with an array size of 100. Think: What would be the simplest strategy for obtaining an array of random integers?
3. Implement the display and selectionSort methods. Think: What could be done to limit the body of the display method to a single statement? Confirm by observation that the elements are being ordered by your selectionSort method.

We can get an idea of the amount of time the Selection Sort algorithm takes by invoking the System.currentTimeMillis() method.

4. Modify your driver to determine and display the time taken, in seconds (to 3 decimal places), for the selectionSort method to perform its task.
5. Increase the size of the array to 20 000 and run your code again.

6. Modify your driver to produce timing results for array sizes from 20 000 to 100 000, increasing by 20 000 each time. Format your output as follows,

   

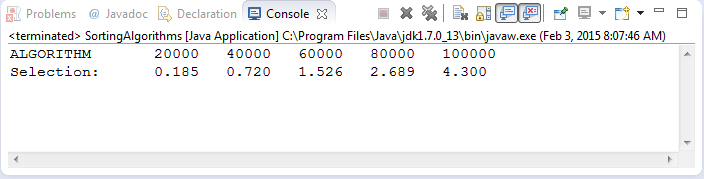
7. Do the times YOU obtain seem reasonable? Consider changes to your driver to address any concerns. Java's System class offers a useful method: System.arraycopy(Object src, int srcPos, Object dest, int destPos, int length)
8. Copy the console data to the clipboard and paste it in a blank Excel worksheet
9. Develop an appropriately-annotated line chart to confirm the Big O of this algorithm. Save your workbook as Sorts.xlsx. What do your efforts suggest as a possible Big O for the Selection sort? Explain why this could have been expected.

Insertion Sort

10. Add the method private static int[] insertionSort(int [] data) to your SortingAlgorithms class that implements the Insertion Sort.
11. Modify your sort method to return the result of a call to your insertionSort(in[] data) method and record the time for the similar array sizes to your Excel worksheet. Add the new data series to the Chart and compare. Conclusion?

Merge Sort and Quicksort

12. Add the method private static void mergeSort(int [] data) to your SortingAlgorithms class that implements the Merge Sort.
13. Add a call to the method from your driver and records the times for the similar array sizes to yor Excel Worksheet. Add the new data series to the Line Chart and compare. Conclusion?
14. Add the method private static void quickSort(int [] data) to your SortingAlgorithms class that implements the QuickSort.
15. Add a call to the method from your driver and records the times for the similar array sizes to yor Excel Worksheet. Add the new data series to the Line Chart and compare. Conclusion?