Recursion Studies

It is virtually impossible to provide practical programming solutions to a variety of complex problems without recursion. As such, it is an indispensable programming strategy.

The Key

Successful implementation of a recursive solution depends on your ability to define a recursive solution on paper. For example, the power function, xⁿ can be defined non-recursively as,

Defined recursively, we write,

From (1), the implementation is straightforward. Successful recursive solutions arise from the programmer being able to express a definition similar to (1) for each new problem, that includes both the general inductive substitution expression and a basis or stopping condition.

Examples

The table below suggests algorithms that lend themselves to recursive solutions. Develop methods to satisfy the stated purpose and a sample driver to test them.

Grade	Topic	Type	Purpose
11	Sum	Num	Determines `1+2+3+...+n=Sigma_{i=1}^n i`
11	Factorial	Num	Determines `n\times (n-1)\times (n-2)\times...\times3\times2\times1 = n! = Pi_{i=1}^n i`
11	Pascal's Triangle	Num	Determines elements from Pascal's Triangle
11	Fibonacci	Num	Determines and displays terms from the Fibonacci sequence: `1,1,2,3,5,...` See: The nth term formula of the Fibonacci sequence from a quadratic equation
11	Square Root	Num	approximate a square root by guessing
11	GCD	Num	Euclid's algorithm for determining the greatest common divisor
11	Base Conversion	Num	Converts decimal numbers to any other base (<10)
11	Reverse Bits	Num	Reverse the bits of register (16-bit)
11	Palindrome	Char	Reverses the order of the characters in a string
11	Matching Brackets	Char	Uses a stack to confirm matching brackets in an expression
12	Root finding	Num	Uses Newton's Method to determine a root of a function, `x_{i+1}=x_i-\frac{f(x_i)}{f'(x_i)}`
12	Successive Approximation	Num	Anaolog to Digital Conversion (Similar to Newton's Method)
13	Determinants	Num	Solves determinants recursively for use in Cramer's Rule

* Mathjax Reference: https://math.meta.stackexchange.com/questions/5020/mathjax-basic-tutorial-and-quick-reference

---

Improved Power Method (Adapted from Data Structures and Algorithms, Goodrich and Tamassia)

The complexity of the power function function above is O(n). We can compute the power function much faster than this however, by using the following alternative recursive definition, which employs a squaring technique as illustrated by the following examples,

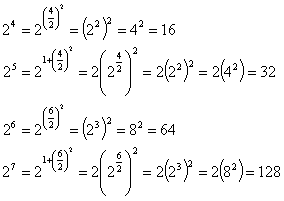
A close examination of the examples suggests that each recursive call to divides the exponent by two. Thus, there are O(log n) recursive calls, not O(n). That is, by combining recursion with the squaring technique, we reduce the running time for the computation of the power function from O(log n) to O(n) - a significant improvement.

Task. Look closely at the examples and compose a piecewise definition for xn similar to (1) above. (This is typically the key to a successful recursive implementation) Implement your definition above by completing the body of the power() method in this code.

---