2010-2011 ICS3U SOFTWARE ENGINEERING
TASKS |
TASK 'CHALLENGE' RATING (offered
to assist you with project management strategies) |
||
Routine |
Typically some deep thinking required,
but not necessarily a lot of coding. |
|
Hard |
Likely involves either a multiplicity of new concepts
and/or new mathematical concepts or algorithms. |
|
Really Hard |
Start immediately, think
hard, employ a stepwise refinement strategy and post concerns
as required. |
|
![]() The
Game of Life.
John Conway introduced the world to one of the most studied algorithms within the Cellular Automata family in the October 1970 issue of Scientific American. Read Wikipedia's explanation of the simple rules for propagation. In the applet to the right, I've colour-coded the cells as Birth, Survival and Death. Explore the game through either or both of the Explore links on the course page. Give yourself time to enjoy how such an elegantly simple set of rules can produce such fascinating outcomes.
The
Game of Life.
John Conway introduced the world to one of the most studied algorithms within the Cellular Automata family in the October 1970 issue of Scientific American. Read Wikipedia's explanation of the simple rules for propagation. In the applet to the right, I've colour-coded the cells as Birth, Survival and Death. Explore the game through either or both of the Explore links on the course page. Give yourself time to enjoy how such an elegantly simple set of rules can produce such fascinating outcomes.
Task.
![]() Insertion Sort. In a process similar to our development of an animated presentation of the Selection Sort, work out an implementation for the Insertion Sort. Update your website wth the Framework applet that includes the two search algorithms (Sequential and Binary) as well as the two sort algorithms (Selection and Insertion).
Insertion Sort. In a process similar to our development of an animated presentation of the Selection Sort, work out an implementation for the Insertion Sort. Update your website wth the Framework applet that includes the two search algorithms (Sequential and Binary) as well as the two sort algorithms (Selection and Insertion).
![]() Selection Sort. Together, we will integrate an animated presentation of the Selection Sort into our Framework Applet. As with the searching algorithms, our Sort classes will implement the Drawable interface. Examine the animated gif (below right) assembled from saved frames. I'll show you the technique for saving bufferedImage objects to disk into either .gif. jpg, or .bmp formats.
Selection Sort. Together, we will integrate an animated presentation of the Selection Sort into our Framework Applet. As with the searching algorithms, our Sort classes will implement the Drawable interface. Examine the animated gif (below right) assembled from saved frames. I'll show you the technique for saving bufferedImage objects to disk into either .gif. jpg, or .bmp formats.
| Framework UML v2.0 | Animated Selection Sort |
|---|---|
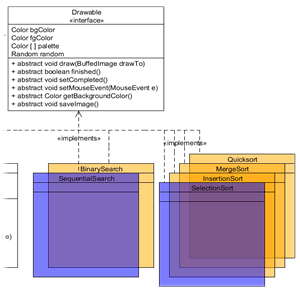 |
 |
Task.
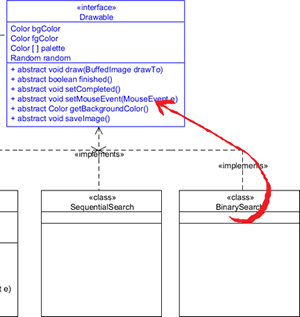
Task.

![]() Project Framework. Anywhere, anytime access to your coding achievements will be useful to you. Therefore, the remaining projects for this year will be
embedded within your Project Framework applet and mounted on your home page.
Project Framework. Anywhere, anytime access to your coding achievements will be useful to you. Therefore, the remaining projects for this year will be
embedded within your Project Framework applet and mounted on your home page.
Task.

![]() PART 1: Bingo Card. Create a project called Bingo1 and add
this driver. As you can see, the driver simply instantiates and
displays an instance of a BingoCard class.
Provide an implementation of the BingoCard class
that follows this
basic UML design. You output should
look similar to the capture below.
PART 1: Bingo Card. Create a project called Bingo1 and add
this driver. As you can see, the driver simply instantiates and
displays an instance of a BingoCard class.
Provide an implementation of the BingoCard class
that follows this
basic UML design. You output should
look similar to the capture below.
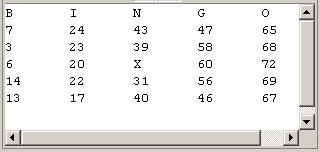
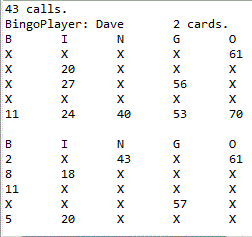
Task. Create a new project entitled, Bingo2 and drop in this driver. Configure the project's Build Path by adding the Project Bingo1. In this way, you will only have one BingoCard class on your computer. Create a BingoPlayer class that matches this UML diagram to the letter! Sample output appears to the right.
![]() PART 3. Bingo
Game. The
final stage of the Bingo trilogy should be obvious. You are to simulate
a multi-player Bingo
Game. In the past few lessons you have been introduced to Java's ArrayList<E> class
that offers users a suite of methods for the convenient manipulation of arrays.
So, just as the Integer and Double classes
are wrapper classes for ints
and doubles respectively, the ArrayList<E> class
can be thought of as a wrapper for arrays.
PART 3. Bingo
Game. The
final stage of the Bingo trilogy should be obvious. You are to simulate
a multi-player Bingo
Game. In the past few lessons you have been introduced to Java's ArrayList<E> class
that offers users a suite of methods for the convenient manipulation of arrays.
So, just as the Integer and Double classes
are wrapper classes for ints
and doubles respectively, the ArrayList<E> class
can be thought of as a wrapper for arrays.
Task. Create a project called Bingo3. Add the Bingo2 and Bingo1 Projects to Bingo3's Build Path. Add the text file Players1011.txt to the Project's root. Examine the contents of the file. The data file has a number of records that contain two fields each (the player's name and number of cards), separated by a tab. Using much of Bingo2's driver code, create the driver for Bingo3 that uses the data from Players1011.txt to house the list of players. Then, undertake a Bingo game in which all players are involved until a winner is identified. For verification, print out only the winning player(s) and all of his cards. Note, I will use a different Players1011.txt file (with the same field structure) when I evaluate your project.

![]() The Sieve of Eratosthenes. There
is no known efficient procedure for finding prime numbers. A classical, but tedious,
method attributed to Eratosthenes (276 - 196 BC), can be described as follows.
First, write down a list of integers, paired with true values,
The Sieve of Eratosthenes. There
is no known efficient procedure for finding prime numbers. A classical, but tedious,
method attributed to Eratosthenes (276 - 196 BC), can be described as follows.
First, write down a list of integers, paired with true values,
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 T T T T T T T T T T T T T T T T T T T
Then mark all multiples of 2 by switching its true to false,
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 T T F T F T F T F T F T F T F T T T F
Move to the next unmarked number, which in this case is 3, then mark all its multiples:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 T T F T F T F F F T F T F F F T F T F
Continue in this fashion, marking all multiples of the next unmarked number until there are no new unmarked numbers. The numbers which survive this marking process (the Sieve of Eratosthenses) are primes.
Task. Write the class, Sieve, that will implement the Sieve of Eratosthenes and determine the prime numbers from 2 to n-1, where the integer n is determined by the user.
Your program will create an array of length n, initializing all cells to true. Starting with array index 2, (ignore index 0 and index 1), every time an array element is found to be true, loop through the remainder of the array and set to false every element whose index is a multiple of the starting index.
At the end of the implementation, array elements that remain true have an index which is a prime number. Display the prime numbers to the console.
We'll try something new this week. Students can submit either Trigonometric Functions as defined below or Exercise P6.1, CurrencyConverter. In the case of the latter, a 30% discount will be applied to the earned mark.
![]() Trigonometric
Functions. The Math class
offers a wide variety of mathematical tools for use by clients. (the
trigonometric functions are members of a class of functions known as transcendentals
in that the exact value can't be computed precisely, but rather is approximated,
typically through the addition of successive terms in a well-defined series)
Trigonometric
Functions. The Math class
offers a wide variety of mathematical tools for use by clients. (the
trigonometric functions are members of a class of functions known as transcendentals
in that the exact value can't be computed precisely, but rather is approximated,
typically through the addition of successive terms in a well-defined series)
Degrees (d) to Radians (r). The Math class offers two built-in conversion methods, toDegrees(double angrad) and toRadians(double angdeg) for your convenience that implement the following definitions,
![]()
Infinite Series Approximations of the trigonometric functions sin(x) and cos(x), x in R (radians)
![]()
![]()
Task.
public static double sin( double angle)
and
public static double cos( double angle)
based on the two series above that can be used to confirm the accuracy of the built-in methods of the Math class. If your NumericalMethods class works properly, the project will yield the output below (up to 360°).

![]() Line. Consider Exercise P5.15 on
page 224, henceforth known as,
LineTest. Review this sample output to guide your development of this project.
Line. Consider Exercise P5.15 on
page 224, henceforth known as,
LineTest. Review this sample output to guide your development of this project.
Task.

![]() iTunes1. To gain familiarity with boolean operators and expressions, we'll query a database (text file) for data that match specific criteria.
iTunes1. To gain familiarity with boolean operators and expressions, we'll query a database (text file) for data that match specific criteria.
Task.
![]()
Now, construct boolean queries to determine the number of matches for each of the stated criteria below. (Note: You many wish to open Music1.txt in Excel to confirm the data sets your queries produce)
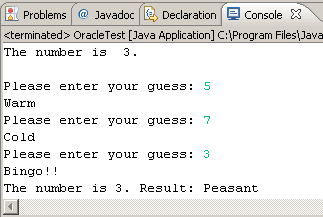
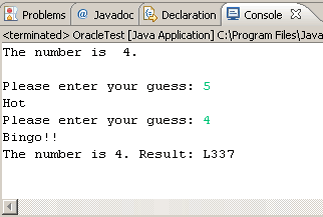
Table 1. Each Guess |
Table 2. Honour |
||
| Guess |
Result |
Number of Guesses |
Level |
exactly |
Bingo!! |
1 |
Jedi |
within 1 |
Hot! |
2 |
L337 |
within 2 |
Warm |
3 |
Peasant |
otherwise |
Cold |
otherwise |
n00b |
 Task.
You are to give the user no more than three attempts
to discover the secret digit. Summarize each game by labeling the player's
outcome
according to Table 2. In addition to printing the label, also display
the secret number for confirmation purposes (not
before as in the two examples). Use as many elements of good
coding conventions and style that
we have discussed and submit OracleTest.java and
Oracle.java to handin by the
deadline.
Task.
You are to give the user no more than three attempts
to discover the secret digit. Summarize each game by labeling the player's
outcome
according to Table 2. In addition to printing the label, also display
the secret number for confirmation purposes (not
before as in the two examples). Use as many elements of good
coding conventions and style that
we have discussed and submit OracleTest.java and
Oracle.java to handin by the
deadline.
 |
 |

![]() Comparing
Objects: Prioritizer. (In class) You are aware that the equality operator
(==)
is
not used to compare the values of two objects. The preferred technique is to
add
the
method, public
int compareTo(Object other)to any class that requires a signed integer
ranking
between the implicit parameter (this)
and the explicit parameter (other)
instances of the
class.
Comparing
Objects: Prioritizer. (In class) You are aware that the equality operator
(==)
is
not used to compare the values of two objects. The preferred technique is to
add
the
method, public
int compareTo(Object other)to any class that requires a signed integer
ranking
between the implicit parameter (this)
and the explicit parameter (other)
instances of the
class.
Part A. Comparing Assignment Objects.
Part B. Automated Prioritizer. To automate the prioritization of assignments that require completion, you are to develop software to tell you what your highest priority task is.



![]() Drow2. In the second instalment of the Drow trilogy you are to demonstrate
the ability to read the contents of a user-selected text file and display it
in a graphic context.
Drow2. In the second instalment of the Drow trilogy you are to demonstrate
the ability to read the contents of a user-selected text file and display it
in a graphic context.
Task.
![]() IP
Address. (This assignment will give you practice manipulating numerical
and String data
in the analysis of an Internet Protocol (IP) address) The purpose of this
assignment is to allow the user to enter an IPv4 address in dotted-decimal
form and the software
will convert it to it's binary equivalent (if it is valid). You can restrict
the reasons for an invalid address to either an incorrect number of octets
(there
should be exactly 4) or the value of any given octet is out of range (it
must be between 0 and 255, inclusive). Take a test
drive of the final project. In addition, you are
encouraged to look carefully and the driver's
use of JOptionPane's
input and output dialog boxes. Use these dialogs where appropriate in the
assignments
ahead.
IP
Address. (This assignment will give you practice manipulating numerical
and String data
in the analysis of an Internet Protocol (IP) address) The purpose of this
assignment is to allow the user to enter an IPv4 address in dotted-decimal
form and the software
will convert it to it's binary equivalent (if it is valid). You can restrict
the reasons for an invalid address to either an incorrect number of octets
(there
should be exactly 4) or the value of any given octet is out of range (it
must be between 0 and 255, inclusive). Take a test
drive of the final project. In addition, you are
encouraged to look carefully and the driver's
use of JOptionPane's
input and output dialog boxes. Use these dialogs where appropriate in the
assignments
ahead.
 |
 |
Task.
Suppose the goal is to determine the square root of 20, call it x. Since 16<20<25, we know the answers lies somewhere between 4 and 5, likely closer to 4. In some situations, we could stop here, offering 4 as the square root of 20. But, like any good competition, a better approximation would be impressive. Try this. If we let x=4, Newton suggested,
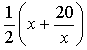
would result in an improved approximation. A quick calculation yields a result of 4.5. Squaring 4.5 produces 20.25. Not bad. Newton's prediction appears to be correct. Ok, from 4 we calculated 4.5. Is this the end of it? Is this the best approximation we can come up with?
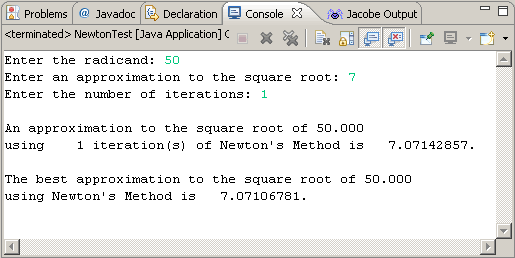
Task. Create a project called NewtonTest and drop in this driver. Next, create a static NumericalMethods class and implement (at least) the following two methods,
/**
* sqrt returns an approximation to the square root of the number a,
* given an initial guess of x, using n iterations of Newton's Method
* @param a the radicand
* @param x the initial approximation to the square root of a
* @param n the number of iterations of Newton's Method
*/
public static double sqrt(double a, double x, int n)
and
/**
* sqrt returns THE BEST approximation to the square root of the number a,
* given an initial guess of x, using Newton's Method
* @param a the radicand
* @param x the initial approximation to the square root of a
*/
public static double sqrt(double a, double x)
Your code should yield the output below. Submit your NumericalMethods class by the deadline.
![]() Drow.
(This is the first of a 3-part assignment)
Read Exercise
P3.8 on page 127. Review the How To 3.1 Implementing a Class Section
on pp.99-101. Recall Stepwise Refinement from last year.
Drow.
(This is the first of a 3-part assignment)
Read Exercise
P3.8 on page 127. Review the How To 3.1 Implementing a Class Section
on pp.99-101. Recall Stepwise Refinement from last year.
Task.
 From the description of the Exercise, identify the methods and instance
fields that are required.
From the description of the Exercise, identify the methods and instance
fields that are required.![]() Toyota Logo Revisited. In preparation for next week's larger graphics
application, you are asked to make a few improvements to your previous Toyota
application.
Toyota Logo Revisited. In preparation for next week's larger graphics
application, you are asked to make a few improvements to your previous Toyota
application.
Positioning and Proportion Improvements.
Dimension dim = getSize();Determining the coordinates of the center of the panel is simply a matter of averaging the two measures, while accounting for the height of the title bar. With the center known, constructing the rectangular bounding areas of the three ellipses is straightforward. The only concern you have is allowing enough room at the bottom for the TOYOTA name.
The FontMetrics class of java.awt encapsulates information about the measure (metric) of a given font. Coincidentally, the Graphics2D class has method called getFontMetrics() that returns a FontMetric object that can be manipulated to reveal the bounds of a given String object within the current graphics environment in the form of a Rectangle2D object.
![]()
 Toyota
Logo.
For your first Java2D graphics assignment you are asked to recreate
the
familiar
logo. Create a graphical application called Toyota that
renders the logo to the right as closely as you can. Some of the areas you will
need
to
investigate
include,
Toyota
Logo.
For your first Java2D graphics assignment you are asked to recreate
the
familiar
logo. Create a graphical application called Toyota that
renders the logo to the right as closely as you can. Some of the areas you will
need
to
investigate
include,
Note. An important consideration is the scalability of your rendering. As can be seen from this example, as the frame is resized, the image remains proportional, centered horizontally and scaled to ensure it remains entirely within the panel.
![]() Exercise P2.3. Create a project called, ExP2_3 and complete
the exercise
as
specified at the bottom pf Page 75 with the additional requirement that the four parameters required by the Rectangle constructor of the original rectangle are randomly generated over the following intervals: the coordinates of the top left corner are between 10 and 50 inclusive, and the width and height are between 20 and 100, inclusive.
Exercise P2.3. Create a project called, ExP2_3 and complete
the exercise
as
specified at the bottom pf Page 75 with the additional requirement that the four parameters required by the Rectangle constructor of the original rectangle are randomly generated over the following intervals: the coordinates of the top left corner are between 10 and 50 inclusive, and the width and height are between 20 and 100, inclusive.
![]() Finally, for the motivated, a range of bonus points will be awarded for those submissions that render the rectangles graphically. A straightfoward discussion of Graphical Applications and Frame Windows can be found on pp. 58-63.
Finally, for the motivated, a range of bonus points will be awarded for those submissions that render the rectangles graphically. A straightfoward discussion of Graphical Applications and Frame Windows can be found on pp. 58-63.